2015-02-27
660
В ряде задач детальное знание элементов матрицы высшего порядка несущественно, и решение может быть получено при изучении степеней так называемой скелетной матрицы, отличающейся тем, что она имеет существенно более простые элементы. Для автомата Men состояниями скелетная матрица составляется из n строк и n столбцов, обозначаемых так же, как в [М], и обозначается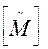 
. Элемент (i, j) матрицы 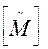обозначается 
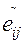. Если b ij обозначает дугу, ведущую из состояния σ i в состояние σ j в автомате М, то 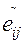определяются так:
Тогда матрица 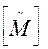может быть построена из [М] или 
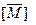посредством замены каждого ненулевого элемента в этих матрицах на 1.
Теорема 2.5. Элемент (i, j) матрацы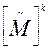 
, где k = l, 2,..., равен числу путей длины k, ведущих из состояния σ i в состояние σ j в автомате М.
Доказательство. Для k = 1 теорема справедлива по построению. Предположим, что теорема справедлива для k; тогда элемент (u, i) матрицы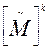 
, обозначаемый 
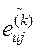представляет число путей длины k, ведущих из σ u в σ j. Элемент (i,j) матрицы =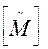 
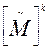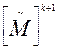определяется формулой
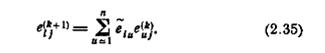
В выражении (2.35) 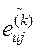умножается на 1, если в σ u можно попасть из σ i, пройдя только одну дугу, и умножается на нуль в противном случае. Следовательно, элемент 
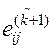равен числу путей длины k + l, ведущих из σ i в σ j. По индукции теорема верна для k > 0.
Сжатая цифровая форма скелетной матрицы может быть использована в задачах, где важно знать наличие или число путей между определенными состояниями, но не обязательно знать, какие дуги входят в каждый путь. Можно определить число минимальных путей, ведущих из σ i в σ j, посредством построения 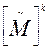для последовательных значений k ≤ n—1; если элемент (i, j) равен нулю в 
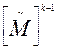, но не равен нулю в 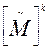, то элемент (i, j) матрицы 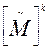представляет собой число минимальных путей длины k; если элемент (i, j) равен нулю в 
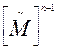, то путь между σ i и σ j не существует.
Матрицы (2.36) — (2.38) иллюстрируют построение скелетной матрицы для автомата A1, изображенного на рис. 2.2, и построение по этой матрице матриц второй и третьей степени. Из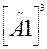 
видно, например, что в состояние 5 нельзя попасть из состояния 2 ни одним путем, имеющим длину меньше 4, и что в состояние 1 можно попасть из состояния 4 девятью различными путями длины 3.
Следует заметить, что, поскольку одна дуга может соответствовать более чем одной паре вход-выход, то ненулевой элемент (i, j } матрицы 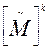не обязательно представляет число всех входных последовательностей длины k, которые переводят автомат М из состояния σ i в σ j. Если представляет интерес число входных последовательностей, переводящих M из σ i в σ j, а не число путей, то можно определить модифицированную скелетную матрицу, обозначаемую через 
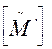, элемент (i, j) которой, обозначаемый 
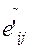, определяется так:
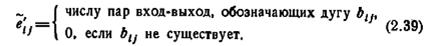
При таком определении матрица 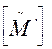может быть построена из [ М ] заменой каждого ненулевого элемента в [ М ] числом пар вход-выход, содержащихся в этом элементе. Матрицу 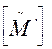можно рассматривать как скелетную матрицу автомата М, где каждая дуга, обозначенная h парами вход-выход, заменена h параллельными дугами, каждая из которых обозначена одной парой вход-выход. Благодаря такой замене число дуг, содержащихся в каком-либо пути, становится равным числу пар вход-выход, содержащихся в обозначениях всех дуг этого пути. Таким образом, элемент (i, j) матрицы 
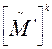должен совпадать с общим числом входных последовательностей длины k, которые переводят М из σ i в σ j.
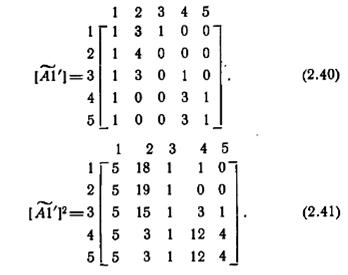
Матрицы (2.40) и (2.41) иллюстрируют построение модифицированной скелетной матрицы автомата А1 (рис. 2.2) и построение по этой матрице матрицы второй степени. Из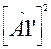 
видно, например, что имеются три кратчайшие вход-входные последовательности, которые переводят А1 из состояния 4 в состояние 2, и что есть 12 входных последовательностей длины 2, которые переводят А1 из состояния 5 в состояние 4.
