Задача распознавания повреждений

Значительный практический интерес представляет задача распознавания повреждения, которое вызвало неисправность автомата. В связи с этой задачей удобно рассматривать поврежденный автомат как самостоятельный автомат. При этом задача распознавания поврежденного автомата, в котором повреждение предполагается относящимся к известному классу повреждений, сводится к задаче распознавания автомата, относящегося к известному классу автоматов. Из результатов § 5.3 следует, что повреждение всегда может быть определено, если класс, к которому относится поврежденный автомат, является исключительным классом.

Чтобы проиллюстрировать процедуру распознавания автомата вообще и распознавания повреждения в частности, рассмотрим автомат A24, представленный таблицей 5.1

Известно, что автомат A24 неисправен и что в результате повреждения при приложении к автомату в одном из его состояний входного символа а на его выходе вместо О появляется 1. Поврежденный автомат A24 может быть одним

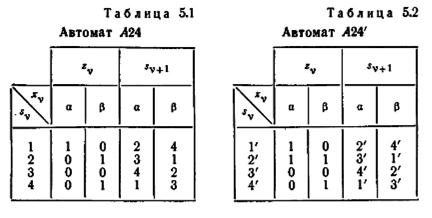
из автоматов A24', A24" и A24'", представленных таблицами 5.2, 5.3 и 5.4 соответственно. Чтобы определить, составляют ли автоматы A24', A24" и А24'" исключительный класс, следует произвести эквивалентное разбиение для автомата ∆(A24', A24" и A24'"), т. е. для расщепляемого автомата, построенного из автоматов A24', A24" и A24'".

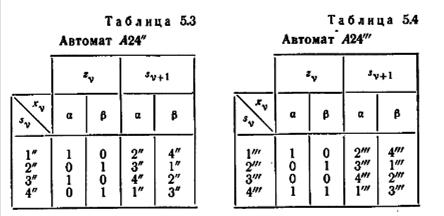
Разбиение может быть выполнено с помощью таблицы пар, как показано в таблице 5.5. Из этой таблицы видно, что эквивалентными в автомате ∆(A24', A24", A24'") являются только пары {1", 3"} и {2", 4"}. Следовательно, автомат A24"

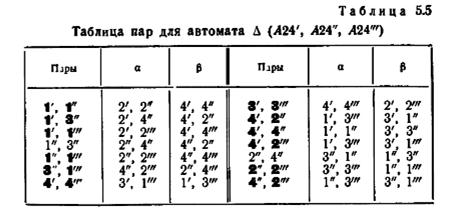
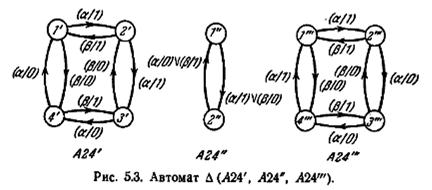
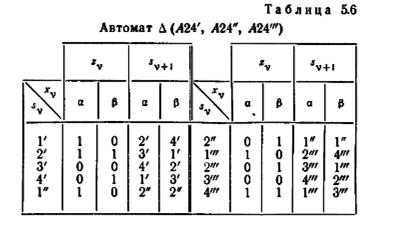
не является минимальным, и ни одно состояние одного автомата не является эквивалентным никакому состоянию другого автомата. Таким образом, после того как автомат A24" будет представлен своей минимальной формой, автомат ∆(A24', A24", A24'") становится минимальным и притом таким, что автоматы A24', A24" и A24'" (все в своих минимальных формах) образуют исключительный класс. Таблица переходов и граф переходов автомата ∆(A24', A24". A24'") приведены на рис. 5.3 и в таблице 5.6 (автомат A24" дан в своей минимальной форме).

Теперь задача определения повреждения в автомате A24 сведена к задаче определения конечного состояния поврежденного автомата A24 или к задаче проведения установочного эксперимента над автоматом ∆(A24', A24". A24'").

Эксперимент для распознавания повреждения описан в таблице 5.7, где предполагается, что начальным состоянием

автомата A24 является состояние 2 и что в результате повреждения при приложении к автомату входного символа а в состоянии 4 на выходе получается 1. Тогда истинным автоматом является А24'", а истинным начальным состоянием— 2'" (это, конечно, экспериментатору сначала не известно). Первый столбец таблицы 5.7 содержит в качестве руководства читателю истинное состояние A24"' на различ-

ных стадиях эксперимента по распознаванию. В соответствии с алгоритмом 5.1 сначала проведем регулярный условный установочный эксперимент для автомата A24' с множеством допустимых начальных состояний {1', 2', 3', 4'}. В конце этого эксперимента оказывается, что если испытуемый автомат есть автомат A24', то его конечным состоянием должно быть состояние 2'. Далее проводим регулярный условный установочный эксперимент для A24" с множеством допустимых начальных состояний {1", 2"}. В конце этого эксперимента может быть сделано заключение о том, что если испытуемый автомат есть A24", то его конечным состоянием должно

быть 1". Затем проводим регулярный условный установочный эксперимент для автомата A24'" с множеством допустимых начальных состояний {1'", 2'", 3'", 4"'}, который устанавливает, что конечное состояние должно быть 1'", если испытуемым автоматом является А24'". Тогда в конце третьего установочного эксперимента заданным автоматом может быть A24' в состоянии 1´ (aaa переводит 2' в 1') или A24" в состоянии 1´´´аа переводит 1" в 1"). или A24" в состоянии 1´´´. Поэтому далее проводим регулярный условный установочный эксперимент для автомата ∆(A24', A24". A24'") с множеством допустимых состояний {1', 1", 1'"}, который выявляет, что конечным состоянием является 4'". Так как состояние 4'" принадлежит подавтомату A24'", эксперимент показывает, что испытуемым автоматом является A24'". Таким образом, можно сделать заключение, что имеющее место повреждение вызывает появление 1 вместо 0 при приложении входного символа а к автомату A24 в состоянии 4.

Заметим, что уменьшение длины распознающего эксперимента достигается в том случае, если после приложения каждой подпоследовательности возможно больше состояний автомата ∆(A24', A24". A24'") исключается из рассмотрения в качестве конечных. Например, после приложения первым входного символа β и получения 1 на выходе состояния 2", 2'" и 4'" (в дополнение к состояниям 2' и 4') могут быть исключены из числа конечных состояний. В результате второй установочный эксперимент может быть опущен, а третий установочный эксперимент укорочен.