Общая задача распознавания автомата

Будем говорить, что автомат является распознанным, если определена (с точностью до изоморфизма) его минимальная форма путем измерений на его внешних выводах. Будем говорить, что автомат распознаваем, если он может быть распознан независимо от его начального состояния. Задача распознавания автомата в ее наиболее общей форме состоит попросту в следующем: распознать заданный автомат М. Ниже в этом параграфе мы покажем, что если об автомате М нет достаточной информации, то общая задача распознавания автомата неразрешима.

Теорема 5.1. Автомат М нераспознаваем, если заранее не известен полностью его входной алфавит.

Доказательство. Предположим, что исследователю известно только подмножество, скажем X', входного алфавита X автомата М. Предположим также, что некоторый эксперимент, использующий входную последовательность ε, символы которой выбираются из подмножества X', выявляет, что М имеет минимальную форму М₂, показанную на рис. 5.1.

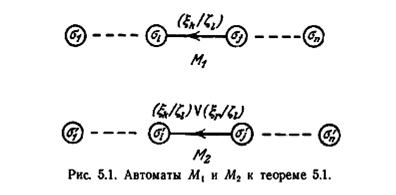
Рассмотрим теперь автомат М₂ (также показанный на рис. 5.1), отличающийся от М₁ только тем, что в М₂ к петле или исходящей дуге всех состояний добавлена пара вход-выход (ξ_r/ξ i), где ξ_r принадлежит X, но не принадлежит X'. Поскольку реакции М₁ и М₂ на последовательность ξ одинаковы, то в результате указанного эксперимента может быть сделан вывод о том, что автомат М — это автомат М₂, с такой же уверенностью, как и вывод, что автомат М — это M₁. Однако, так как автоматы М₁ и М₂ не сравнимы, то они, конечно, не эквивалентны, и, следовательно, предположение о том, что эксперимент выявляет минимальную форму, не может быть доказано. Тогда от противного следует, что если входной алфавит автомата М не полностью известен, то автомат М не может быть распознан.

Теорема 5.2. Автомат М нераспознаваем, если предварительно не известно максимальное число состояний минимальной формы этого автомата.

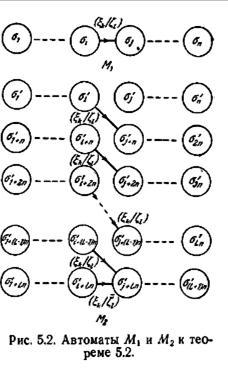
Доказательство. Пусть некоторым экспериментом произвольной, но конечной длины L установлено, что М₁ является минимальной формой автомата М, показанной на рис. 5.2. Пусть автомат Мх имеет множество состояний {σ₁, σ₂,..., σ_n} Рассмотрим автомат М₂ (также показанный на рис. 5.2),

построенный в соответствии со следующими правилами. Автомат М₂ имеет n(L+ 1) состояний σ´₁, σ´₂,..., σ´_n(L+1). Если пара вход-выход (ξ_k/ξ i) обозначает дугу, ведущую от состояния σ_i к состоянию σ_j в автомате M₁ то в автомате М₂ пара (ξ_r/ξ i) также обозначает дугу, ведущую из состояния σ´_i+(u-1)n в состояние σ´_j+un для u=1, 2,..., L; если к автомату М₂ в состоянии σ´_i+Ln приложен входной символ ξ_k, то выходной символ будет 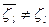; и следующее состояние M₂ будет σ´_i+Ln. Тогда по построению каждая входная последовательность длины L или меньшей вырабатывает одинаковые выходные последовательности в М₁|σ_i,- и в М₂| σ´_i.Однако если прикладывается любая входная последовательность длины L + 1 к М₁|σ_i. и М₂| σ´_i то две выходные последовательности этих автоматов должны различаться последними символами. Таким образом, результат любого конечного эксперимента над автоматом М может быть одинаково присущим как М₁, так и М₂, хотя М₁ и М₂ не эквивалентны. Следовательно, автомат М не может быть распознан никаким конечным экспериментом. Заметим, что если известно максимальное число состояний n автомата М, то автомат М₂ исключается экспериментом длины L такой, что (L+l)n > n. Таким образом, если п известно, то с помощью достаточно длинного эксперимента автомат М может быть распознан.

Итак, можно считать установленным, что необходимым условием распознавания автомата является предварительное

знание его входного алфавита и граничного значения числа состояний его минимальной формы. Предварительное знание выходного алфавита, как мы увидим в дальнейшем, для распознавания автомата не является обязательным.