Формальная постановка «транспортной задачи»

Пусть x_{ij -} количество продукта, перевозимого из пункта А_i в пункт В_j. Требуется определить совокупность из mn величин х_ij», удовлетворяющих условиям:

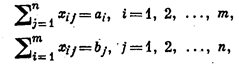
и обращающих в минимум линейную форму:

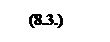
Для решения «транспортной задачи» воспользуемся симплекс–методом, (« симплекс» - в переводе означает «простой», то есть несложный).

Суть метода состоит в приведении задачи к так называемому стандартному виду, при котором обеспечивается равенство ресурсов и потребностей. При этом используется табличная матрица, которая была уже нами представлена в лекции 6 (табл.6.1.)

Все преобразования симплекс-метода мы также будем проводить непосредственно в табличной матрице. Каждое очередное преобразование (итерация, что в переводе означает «шаг») будет продуцировать новый план перевозок, с уменьшенным значением целевой функции. Преобразования-итерации заканчиваются достижением оптимума. Для этого используются два метода: распределительный метод и метод потенциалов.

Каждый из названных методов приводит к оптимальному решению.

Каждый из алгоритмов по названным двум методам начинается спостроения опорного решения, оно является исходным, с которого начинаем реализацию алгоритма. Нахождение опорного решение строится образом, что, в нём число заполненных клеток должно равняться рангу системы r

r = p+ q – 1 (8.4)

Для нахождения опорного решения имеются два метода: метод северо-западного угла и метод минимального элемента.

При этом формулируются и следующие ограничения:

- значения переменных х должны быть больше или равны нулю, поскольку отрицательными объёмы перевозок быть не могут;

- остаётся в силе приведенное определение ранга системы.

Заметим, что общее число базисных решений, которые, могут удовлетворять записанным уравнениям составляет N_б

где:

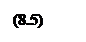
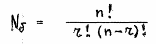
здесь: n - общее число переменных x

r – ранг системы.

Если мы найдём все базисные решения данной системы, то среди них окажутся и такие, в которых базисные переменные будут положительными.. Такие решения называют опорными решениями. При проведении итераций в распределительной таблице следует помнить, что нули базисных переменных обязательно записываются в свободные клетки, в отличие от нулей свободных переменных, которые имитируются пустыми клетками.

Обычно такие базисные нули фигурируют в угловых клетках цикла, и без их использования невозможно организовать целенаправленного циклического преобразования. В целом методика решения данной задачи осуществляется в следующей последовательности: 1. Находим одним из двух методов исходное опорное решение системы, 2. Осуществляем цепочку последовательных циклических преобразований опорного решения симплекс-методом, достигая уменьшения целевой функции. З. Останавливаем процесс при достижении Z _min.