Во многих реальных процессах некоторые факторы взаимодействия могут отсутствовать. И тогда ПФЭ будет обладать избыточностью опытов.
Рассмотрим пути минимизации числа опытов.
Обратимся к уравнению (4.29). Если мы располагаем сведениями о том, что в выбранных интервалах варьирования процесс в статике может быть описан линейной моделью, то достаточно определить три коэффициента b0,b1,b2. В результате остается одна степень свободы, т.к. имеем четыре опыта, а количество констант три. Используем эту степень свободы для минимизации числа опытов. При линейном приближении b12 ® 0 и тогда вектор -столбец х1х2 может быть использован для нового фактора х3.
Таблица 4.4
| Опыт | x0 | x1 | x2 | x3 | y |
| 1 | +1 | +1 | +1 | +1 | y1 |
| 2 | +1 | -1 | +1 | -1 | y2 |
| 3 | +1 | +1 | -1 | -1 | y3 |
| 4 | +1 | -1 | -1 | +1 | y4 |
При этом эксперименте появляются смешанные оценки
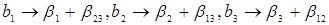 , (4.32)
, (4.32)
т.е. столбцы.
Пример. Допустим х1 и х2х3 между собой неразличимы. Однако парные взаимодействия в линейной модели незначительны. Зато вместо восьми опытов для изучения влияния трех факторов можно поставить только четыре опыта, т.е. вместо ПФЭ 23 мы имеем 23-1. В теории эксперимента 23-1 называют полу- репликой. В общем случае имеют дело с дробной репликой. А факторный эксперимент называют дробным (ДФЭ).
Для уяснения принципа составления МПЭ ДФЭ введено понятие определяющего контраста. Он позволяет определить какие оценки смешаны друг с другом, не изучая МПЭ для выявления совпадающих столбцов. Для этого берут символичное обозначение произведения столбцов равного +1 или -1. Это и называют контрастом. Чтобы определить какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту.
Пример. Пусть имеем три фактора х1,х2,х3. При построении полуреплики 23-1 имеется только две возможности приравнять х3 либо к «+х1х2», либо к «- х1х2» (табл.4.5).
Таблица 4.5
| Опыт | x1 | x2 | x3 | x1x2x3 | Опыт | x1 | x2 | x3 | x1x2x3 |
| 1 | -1 | -1 | +1 | +1 | 1 | -1 | -1 | -1 | -1 |
| 2 | +1 | -1 | -1 | +1 | 2 | +1 | -1 | +1 | -1 |
| 3 | -1 | +1 | -1 | +1 | 3 | -1 | +1 | +1 | -1 |
| 4 | +1 | +1 | +1 | +1 | 4 | +1 | +1 | -1 | -1 |
Возьмем в качестве определяющего контраста 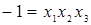 .Тогда
.Тогда 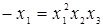 . Учитывая, что
. Учитывая, что 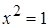 получаем
получаем 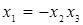 .
.
Теперь возьмем за определяющий контраст 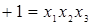 . Получаем:
. Получаем: 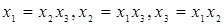 . Эти выражения показывают, что коэффициенты линейного уравнения будут оценками (4.32).
. Эти выражения показывают, что коэффициенты линейного уравнения будут оценками (4.32).
Соотношение, показывающее с какими из эффектов смешан данный эффект, называется генерирующим соотношением.
При выборе полуреплики 24-1 возможны восемь генерирующих соотношений:
1. 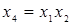
| 5. 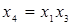
|
2. 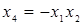
| 6. 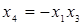
|
3. 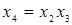
| 7. 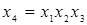
|
4. 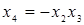
| 8. 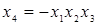
|
Разрешающая способность этих полуреплик различна. Реплики 1-6 имеют по три фактора и носят название планов с расширяющей способностью III (по наибольшему числу факторов в определяющем контрасте). Реплики 7-8 имеют по четыре фактора и обладают максимальной разрешающей способностью. Их называют главными репликами. Всегда стремятся выбрать реплику с наибольшей разрешающей способностью, т.к. чем больше эффектов взаимосвязано, тем точнее окажется полученная модель.
Однако, если имеется информация об эффектах взаимодействия, то реплики нужно выбирать с ее учетом.
Реализация МПЭ ДФЭ ничем не отличается от реализации МПЭ ПФЭ. Методика оценки значимости коэффициентов и проверка адекватности модели проводится также как и в ПФЭ.
 2015-02-27
2015-02-27 582
582








