Выведем формулу, позволяющую возводить двучлен (бином) (а+b) в любую целую неотрицательную степень. Это формула бинома Ньютона. Она имеет следующий вид:
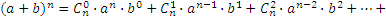
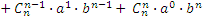 .
.
Докажем данную формулу методом математической индукции по n, где n ≥0.
1. Формула верна при n = 0, 1, 2. В самом деле,
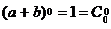 ;
;
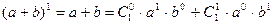 ;
; 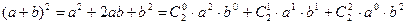 ;
;
2. Пусть формула верна при n = k. Докажем ее при n = k + 1.
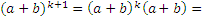
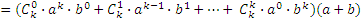 .
.
Раскрыв скобки и сгруппировав слагаемые по степеням а, получим:
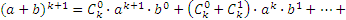
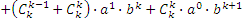 .
.
С учетом свойства 4 и того, что 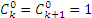 и
и 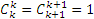 , имеем:
, имеем:
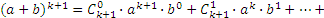
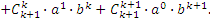
Итак, индукция завершена, значит истинность формулы доказана.
В формуле бинома Ньютона для (а + b)n сумма степеней а и b в каждом слагаемом равна n. Числа 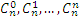 называются биномиальными коэффициентами. При вычислении биномиальных коэффициентов удобно применять треугольник Паскаля.
называются биномиальными коэффициентами. При вычислении биномиальных коэффициентов удобно применять треугольник Паскаля.
В качестве примера найдем: а) (a + b)5; б) (х2-1)4:
а) 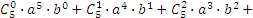
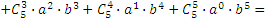
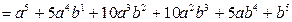 ;
;
б) 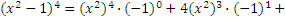
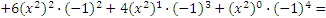
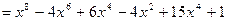
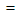
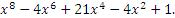
Легко убедиться, что хорошо известные формулы сокращенного умножения для (a + b)2 и (a + b)3 представляют собой частные случаи формулы бинома Ньютона.
Упражнения
1. Докажите:
а) 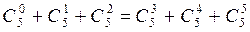 ;
;
б) 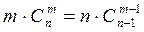 ;
;
в) 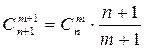 .
.
2. Напишите разложение по формуле бинома Ньютона и упростите при необходимости:
а) (a + b)4; б) (a ― b)4; в) (a + 2b)5; г) (a – 2b)5;
д) (1 + 2x)5; е) 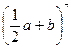 ; ж)
; ж) 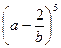 ; з)
; з) 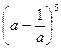 ;
;
и) 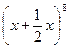 ; к)
; к) 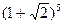 ; л)
; л) 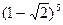 ; м)
; м) 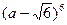 ;
;
н) 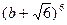 ; о)
; о) 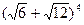 ; п)
; п) 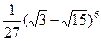 ;
;
ж) 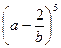 ; з)
; з) 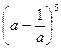 ; и)
; и) 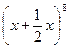 ;
;
к) 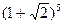 ; л)
; л) 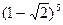 ; м)
; м) 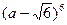 ;
;
3. Найдите:
а) шестой член разложения (1 ― 2z)21;
б) шестой член разложения 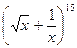 ;
;
в) пятый член разложения 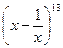 ;
;
г) пятый член разложения 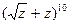 ;
;
д) два средних члена разложения (a3-ab)23;
е) в разложении 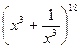 член, не содержащий x;
член, не содержащий x;
ж) в разложении 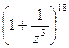 член, не содержащий z;
член, не содержащий z;
з) в разложении 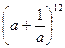 коэффициент при а8;
коэффициент при а8;
и) в разложении 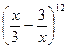 коэффициент при х4;
коэффициент при х4;
к) x, если третий член разложения (х + xlg x)5 равен 106.
 2015-02-27
2015-02-27 4886
4886
