На основе данных, представленных в таблице, провести расчёт аналитических показателей ряда динамики, построение тренда и прогнозирование величины анализируемого социально-экономического явления на последующий временной период методом экстраполяции.
Таблица – Производство молока по районам области (тыс.ц)
| Год | |||||||||
| Значение |
Расчёт абсолютных и относительных показателей ряда динамики необходимо провести в таблице следующей формы:
| Период времени | Уровень ряда | Абсолютный прирост | Темп роста, % | Темп прироста | Абсолютное значение 1 % прироста | |||
| базисный | цепной | базисный | цепной | базисный | цепной | |||
| t | у | Δубаз | Δуцеп | Тр(баз) | Тр(цеп) | Тпр(баз) | Тпр(цеп) | Аi |
| t1 | у1 | |||||||
| t2 | у2 | |||||||
| … | … | |||||||
| tn | уn | |||||||
| Итого | ||||||||
| В среднем |
Средние показатели ряда динамики определить в соответствии с методикой их расчёта и отразить в соответствующей таблице. По результатам расчёта аналитических показателей ряда динамики сформулировать общие выводы.
Для построения тренда необходимо использовать таблицу следующей формы:
| Период времени | Уровень ряда | Расчётные показатели | ||
| ti | уi | t2 | уt | yt |
| t1 | у1 | |||
| t2 | у2 | |||
| … | … | |||
| tn | уn | |||
| Итого |
При построении тренда необходимо использовать уравнение линейной регрессии:
уt = а0 + а1t, где
уt – выровненные значения уровней;
а0 – свободный член уравнения;
а1 – коэффициент регрессии;
t – период времени.
Параметры уравнения (а0, а1) находятся путём составления и решения системы нормальных уравнений способом наименьших квадратов:
 Σу = nа0 + а1Σt
Σу = nа0 + а1Σt
Σyt = a0Σt + a1Σt2
где n – число уровней ряда.
Для определения параметров могут использоваться следующие формулы:
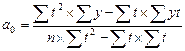
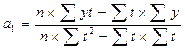
При построении тренда необходимо представить его графическое изображение. На графике следует отобразить фактические уровни ряда и их количественные значения, а также выровненные значения уровней.
 2015-02-27
2015-02-27 923
923








