базовый уровень, время – 3 мин)

Тема: Использование информационных моделей (таблицы, диаграммы, графики).
Перебор вариантов, выбор лучшего по какому-то признаку.

Что нужно знать:

· в принципе, особых дополнительных знаний, кроме здравого смысла и умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется

· полезно знать, что такое граф (это набор вершин и соединяющих их ребер) и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания

· чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки

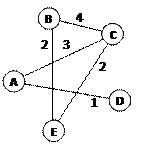
· рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 4 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 4; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет

	A	B	C	D	Е
A
B
C
D
Е

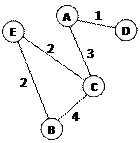
· обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее

· в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)

· желательно научиться быстро (и правильно) строить граф по весовой матрице и наоборот

Пример задания:

Между населёнными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из A в B есть дорога длиной 4 км, а из B в A дороги нет.

	A	B	C	D	E	F	Z
A
B
C
D
E
F
Z

Сколько существует таких маршрутов из A в Z, которые проходят через 6 и более населенных пунктов? Пункты A и Z при подсчете учитывать. Два раза проходить через один пункт нельзя.

Решение:

1) обратим внимание, что числа в таблице нас совсем не интересуют – достаточно знать, что между данными пунктами есть дорога

2) нам нужно найти все пути, которые проходят через 6 и более пунктов, считая начальный и конечный; то есть между A и Z должно быть не менее 4 промежуточных пункта

3) начнем с перечисления всех маршрутов из А, которые проходят через 2 пункта; по таблице видим, что из A можно ехать в B, C и Z; количество пунктов на маршруте будем записывать сверху:

AB
AC
AZ

4) маршрут AZ нас не интересует, хотя он и пришел в конечный пункт, он проходит меньше, чем через 6 пунктов (только через 2!); здесь и далее такие «неинтересные» маршруты из A в Z будем выделять серым фоном

5) теперь ищем все маршруты, проходящие через 3 пункта; из B можно ехать только в C, а из С – в D и Z:

AB	ABC
AC	ACD
ACZ
AZ

6) далее из C едем в D и Z, а из D – в E, F и Z:

AB	ABC	ABCD
ABCZ
AC	ACD	ACDE
ACDF
ACDZ
ACZ
AZ

7) строим следующий уровень только для тех маршрутов, которые ещё не пришли в Z:

AB	ABC	ABCD	ABCDE
ABCDF
ABCDZ
ABCZ
AC	ACD	ACDE	ACDEF
ACDEZ
ACDF	ACDFE
ACDFZ
ACDZ
ACZ
AZ

8) следущие два уровня дают «интересные» маршруты, проходящие через 6 или 7 пунктов:

AB	ABC	ABCD	ABCDE	ABCDEF	ABCDEFZ
ABCDEZ
ABCDF	ABCDFE	ABCDFEZ
ABCDFZ
ABCDZ
ABCZ
AC	ACD	ACDE	ACDEF	ACDEFE
ACDEFZ
ACDEZ
ACDF	ACDFE	ACDFEF
ACDFEZ
ACDFZ
ACDZ
ACZ
AZ

9) на последней схеме зелёным фоном выделены «интересные» маршруты, их всего 6; красным фоном отмечены маршруты, в которых получился цикл – они дважды проходят через один и тот же пункт; такие маршруты запрещены и мы далее их не рассматриваем

10) Ответ: 6.

11) можно было нарисовать схему возможных маршрутов в виде дерева:

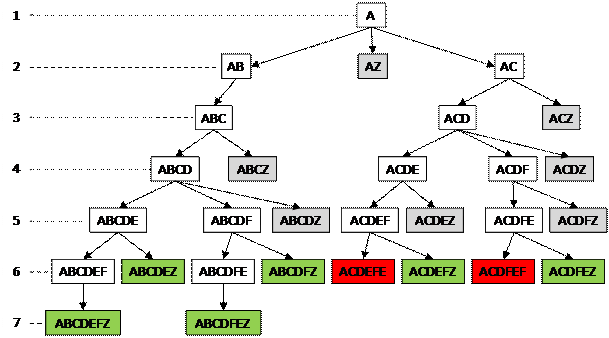
Ещё пример задания:

Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

	A	B	C	D	E	F	G
A
B
C
D
E
F
G

Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

Решение:

1) начнём строить возможные маршруты из пункта A; за 1 шаг можно приехать в B, C или сразу в G (в скобках показаны длины маршрутов):

AB(5), AD(12), AG(25)

заметим, что G – это целевая точка (конечный пункт), поэтому мы уже имеем один полный маршрут длиной 25

2) строим двух шаговые маршруты: из B дальше можно ехать в D (возврат в А неинтересен!)

ABD (5 + 8 = 13)

этот маршрут нет смысла продолжать, поскольку в D можно приехать быстрее: длина уже найденного маршрута AD равна 12

3) из D можно ехать в B и C:

ADB (12 + 8 = 20)

ADC (12 + 2 = 14)

4) третий шаг: маршрут ADB продолжать бессмысленно: из B можно вернуться только в A и D

5) продолжаем маршрут ADC (14):

ADCE (14 + 4 = 18)

ADCF (14 + 5 = 19)

ADCG (14 + 10 = 24)

в последнем варианте мы приехали в конечный пункт, причем новый маршрут имеет длину 24 < 25, то есть, он короче найденного ранее

6) четвёртый шаг: продолжаем маршрут ADCE:

ADCEG (18 + 5 = 23)

и маршрут ADCF:

ADCFG (19 + 5 = 24)

7) других продолжений (без возврата в уже посещённые пункты) нет, поэтому кратчайший маршрут – ADCEG, он имеет длину 23.

8) Ответ: 23.

9) Заметим, что эти рассуждения можно зарисовать в виде дерева возможных маршрутов. После первого шага:

После второго шага:

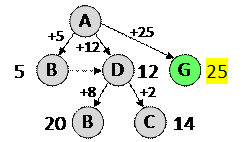
После третьего шага:

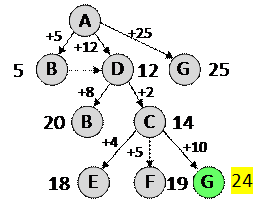
После четвёртого шага:

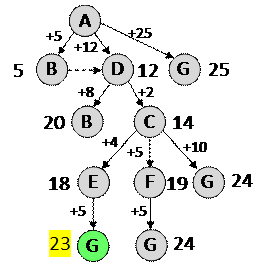
Ещё пример задания:

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

	A	B	C	D	E	F
A
B
C
D
E
F

Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).

Решение (вариант 1, использование схемы):

1) построим граф – схему, соответствующую этой весовой матрице; из вершины А можно проехать в вершины B и C (длины путей соответственно 2 и 4):

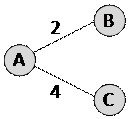
2) для остальных вершин можно рассматривать только часть таблицы над главной диагональю, которая выделена серым цветом; все остальные рёбра уже были рассмотрены ранее

3) например, из вершины В можно проехать в вершины C и E (длины путей соответственно 1 и 7):

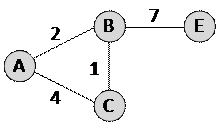
4) новые маршруты из С – в D и E (длины путей соответственно 3 и 4):

5) новый маршрут из D – в E (длина пути 3):

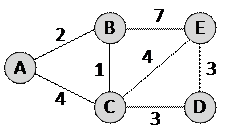
6) новый маршрут из E – в F (длина пути 2):

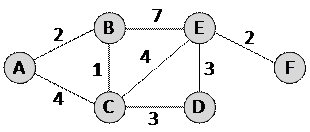
7) нужно проехать из А в F, по схеме видим, что в любой из таких маршрутов входит ребро EF длиной 2; таким образом, остается найти оптимальный маршрут из A в E

8) попробуем перечислить возможные маршруты из А в Е:

А – В – Е длина 9

А – В – С – Е длина 7

А – В – C – D – Е длина 9

А –C – Е длина 8

А –C – B – Е длина 12

А –C – D – Е длина 10

9) из перечисленных маршрутов кратчайший – A-B-C-E – имеет длину 7, таким образов общая длина кратчайшего маршрута A-B-C-E-F равна 7 + 2 = 9

10) таким образом, правильный ответ – 9.

Решение (вариант 2, с начала маршрута):

1) составим граф, который показывает, куда (и как) можно ехать из пункта А, рядом с дугами будем записывать увеличение пути, а рядом с названиями пунктов – общую длину пути от пункта A:

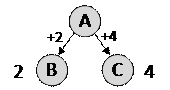
2) видно, что напрямую в пункт F из A не доехать

3) строим граф возможных путей дальше: определяем, куда можно ехать из B и C (конечно, не возвращаясь обратно); из B можно ехать только в A (обратно), в C и в E;

4) узел C уже есть на схеме, и оказывается, что короче ехать в него по маршруту A-B-C, чем напрямую A-C, длина «окольного» пути составляет 3 вместо 4 для «прямого»;
при движении по дороге B-E длина увеличивается на 7:

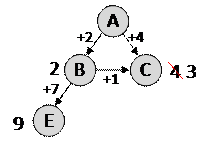
5) строим маршруты из пункта C; кроме A и B, из пункта C можно ехать в D (длина 3) и E (длина 4), причем кратчайший маршрут из A в E оказывается A-B-C-E (длина 7); «невыгодные» маршруты на схеме показывать не будем:

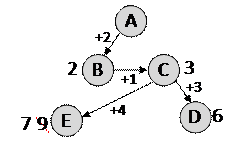
6) из пункта D, кроме как в С и E, ехать некуда; путь D-C – это возврат назад (нас не интересует), путь D-E тоже не интересует, поскольку он дает длину 6 + 3 = 9, а мы уже нашли, что в E из A можно доехать по маршруту длины 7

7) из пункта E можно ехать в F, длина полного маршрута 7 + 2 = 9

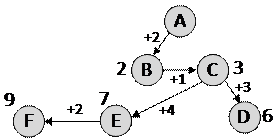
8) Ответ: 9

Решение (вариант 3, с конца маршрута):

1) можно точно так же начинать с пункта F и искать кратчайший маршрут до A; судя по таблице, из F можно ехать только в E:

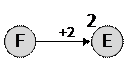
2) из E ведут дороги в B, C и D

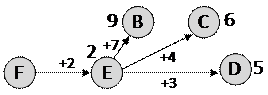
3) из B можно сразу попасть в A, длина пути будет равна 11:

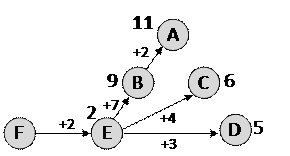
4) из пункта C есть прямая дорога в A длиной 4, таким образом, существует маршрут длиной
6 + 4 = 10

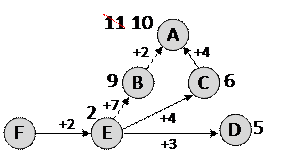
5) кроме того, есть дорога C-B, которая дает маршрут F-E-C-B-A длиной 9

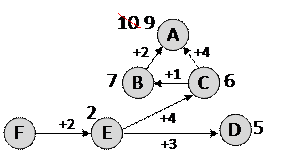
6) рассмотрение пути C-D не позволяет улучшить результат: оптимальный маршрут имеет длину 9

7) Ответ: 9

Возможные ловушки и проблемы: · можно не заметить, что маршруты, проходящие через большее число пунктов, оказываются короче (A-B-C короче, чем A-C, A-B-C-E короче, чем A-B-E)

Пример задания:

Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:

Аэропорт вылета Аэропорт прилета Время вылета Время прилета

СОСНОВО КРАСНЫЙ 06:20 08:35

КРАСНЫЙ ОКТЯБРЬ 10:25 12:35

ОКТЯБРЬ КРАСНЫЙ 11:45 13:30

БЕРЕГ СОСНОВО 12:15 14:25

СОСНОВО ОКТЯБРЬ 12:45 16:35

КРАСНЫЙ СОСНОВО 13:15 15:40

ОКТЯБРЬ СОСНОВО 13:40 17:25

ОКТЯБРЬ БЕРЕГ 15:30 17:15

СОСНОВО БЕРЕГ 17:35 19:30

БЕРЕГ ОКТЯБРЬ 19:40 21:55

Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.

1) 15:40 2) 16:35 3)17:15 4) 17:25

Решение:

1) сначала заметим, что есть прямой рейс из аэропорта ОКТЯБРЬ в СОСНОВО с прибытием в 17:25:

ОКТЯБРЬ СОСНОВО 13:40 17:25

2) посмотрим, сможет ли путешественник оказаться в СОСНОВО раньше этого времени, если полетит через другой аэропорт, с пересадкой

3) можно лететь, через КРАСНЫЙ, но, как следует из расписания,

ОКТЯБРЬ КРАСНЫЙ 11:45 13:30

…

КРАСНЫЙ СОСНОВО 13:15 15:40

путешественник не успеет на рейс КРАСНЫЙ – СОСНОВО, который улетает в 13:15, то есть на 15 минут раньше, чем в КРАСНЫЙ прилетает самолет ОКТЯБРЬ – КРАСНЫЙ

4) можно лететь через БЕРЕГ,

БЕРЕГ СОСНОВО 12:15 14:25

…

ОКТЯБРЬ БЕРЕГ 15:30 17:15

но рейс БЕРЕГ – СОСНОВО вылетает даже раньше, чем рейс ОКТЯБРЬ – БЕРЕГ, то есть, пересадка не получится

5) поскольку даже перелеты с одной пересадкой не стыкуются по времени, проверять варианты с двумя пересадками в данной задаче бессмысленно (хотя в других задачах они теоретически могут дать правильное решение)

6) таким образом, правильный ответ – 4 (прямой рейс).

Возможные ловушки и проблемы: · можно не заметить, что путешественник не успеет на пересадку в КРАСНОМ (неверный ответ 15:40) · можно перепутать аэропорты вылета и прилета (неверный ответ 16:35)

Решение (вариант 2, граф):

1) для решения можно построить граф, показывающий, куда может попасть путешественник из аэропорта ОКТЯБРЬ

2) из аэропорта ОКТЯБРЬ есть три рейса:

ОКТЯБРЬ СОСНОВО 13:40 17:25

ОКТЯБРЬ КРАСНЫЙ 11:45 13:30

ОКТЯБРЬ БЕРЕГ 15:30 17:15

3) построим граф, около каждого пункта запишем время прибытия

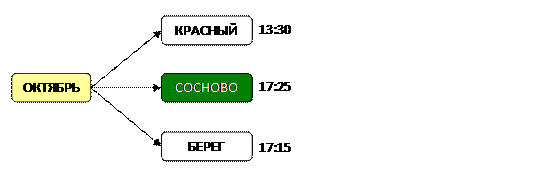
4) проверим, не будет ли быстрее лететь с пересадкой: рейс «КРАСНЫЙ-СОСНОВО» вылетает в 13:15, то есть, путешественник на него не успевает; он не успеет также и на рейс «БЕРЕГ-СОСНОВО», вылетающий в 12:15

5) таким образом, правильный ответ – 4 (прямой рейс).

Еще пример задания:

Грунтовая дорога проходит последовательно через населенные пункты А, B, С и D. При этом длина дороги между А и В равна 80 км, между В и С – 50 км, и между С и D – 10 км. Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге – 20 км/час, по шоссе – 40 км/час.

1) 1 час 2) 1,5 часа 3)3,5 часа 4) 4 часа

Решение:

1) нарисуем схему дорог, обозначив данные в виде дроби (расстояние в числителе, скорость движения по дороге – в знаменателе):

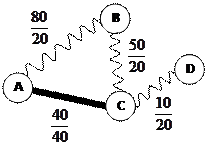
2) разделив числитель на знаменатель, получим время движения по каждой дороге

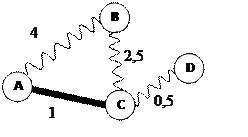
3) ехать из А в B можно

· напрямую, это займет 4 часа, или …

· через пункт C, это займет 1 час по шоссе (из А в С) и 2,5 часа по грунтовой дороге
(из В в С), всего 1 + 2,5 = 3,5 часа

4) таким образом, правильный ответ – 3.

Возможные ловушки и проблемы: · можно не заметить, что требуется найти минимальное время поездки именно в В, а не в С (неверный ответ 1 час) · можно ограничиться рассмотрением только прямого пути из А в В и таким образом получить неверный ответ 4 часа · можно неправильно нарисовать схему

Еще пример задания:

Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

1)	2)	3)	4)
A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е

Решение (вариант 1):

1) нужно рассматривать все маршруты из А в В, как напрямую, так и через другие станции

2) рассмотрим таблицу 1:

· из верхней строки таблицы следует, что из А в В напрямую везти нельзя, только через C (стоимость перевозки А-С равна 3) или через D (стоимость перевозки из А в D равна 1)

	A	B	C	D	Е
A

· предположим, что мы повезли через C; тогда из третьей строки видим, что из C можно ехать в В, и стоимость равна 4

	A	B	C	D	Е
C

· таким образом общая стоимость перевозки из А через С в В равна 3 + 4 = 7

· кроме того, из С можно ехать не сразу в В, а сначала в Е:

	A	B	C	D	Е
C

а затем из Е – в В (стоимость также 2),

	A	B	C	D	Е
Е

так что общая стоимость этого маршрута равна 3 + 2 + 2 = 7

· теперь предположим, что мы поехали из А в D (стоимость 1); из четвертой строки таблицы видим, что из D можно ехать только обратно в А, поэтому этим путем в В никак не попасть:

	A	B	C	D	Е
D

· таким образом, для первой таблицы минимальная стоимость перевозки между А и В равна 7; заданное условие «не больше 6» не выполняется

3) аналогично рассмотрим вторую схему; возможные маршруты из А в В:

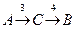· , стоимость 7

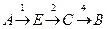· , стоимость 7

· таким образом, минимальная стоимость 7, условие не выполняется

4) для третьей таблицы:

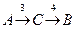· , стоимость 7

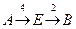· , стоимость 6

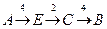· , стоимость 7

· таким образом, минимальная стоимость 6, условие выполняется

5) для четвертой:

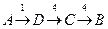· , стоимость 9

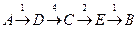· , стоимость 8

· минимальная стоимость 8, условие не выполняется

6) условие «не больше 6» выполняется только для таблицы 3

7) таким образом, правильный ответ – 3.

Возможные ловушки и проблемы: · метод ненагляден, легко запутаться и пропустить решение с минимальной стоимостью

Решение (вариант 2, с рисованием схемы):

1) для каждой таблицы нарисуем соответствующую ей схему дорог, обозначив стоимость перевозки рядом с линиями, соединяющими соседние станции:

1)	2)	3)	4)
A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е	A B C D Е A           B           C           D           Е

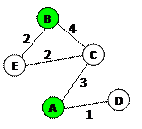
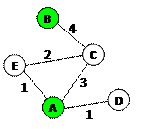
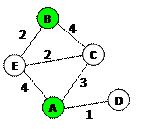
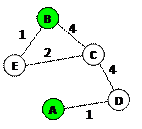
2) теперь по схемам определяем кратчайшие маршруты для каждой таблицы:

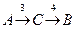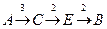1: или , стоимость 7

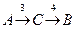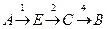2: или , стоимость 7

3: 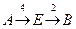, стоимость 6

4: 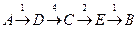, стоимость 8

8) условие «не больше 6» выполняется только для таблицы 3

9) таким образом, правильный ответ – 3.

Возможные ловушки и проблемы: · нужно внимательно строить схемы по таблицам, этот дополнительный переход (от табличных моделей к графическим) повышает наглядность, но добавляет еще одну возможность для ошибки · наглядность схемы зависит от того, как удачно вы выберете расположение ее узлов; один из подходов – сначала расставить все узлы равномерно на окружности, нарисовать все связи и посмотреть, как можно расположить узлы более удобно · по невнимательности можно пропустить решение с минимальной стоимостью

Еще пример задания [1]:

Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:

Аэропорт вылета Аэропорт прилета Время вылета Время прилета

ВОСТОРГ ГОРКА 16:15 18:30

ОЗЕРНЫЙ ЗАРЯ 13:40 15:50

ОЗЕРНЫЙ ВОСТОРГ 14:10 16:20

ГОРКА ОЗЕРНЫЙ 17:05 19:20

ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20

ЗАРЯ ОЗЕРНЫЙ 16:20 18:25

ВОСТОРГ ЗАРЯ 14:00 16:15

ЗАРЯ ГОРКА 16:05 18:15

ГОРКА ЗАРЯ 14:10 16:25

ОЗЕРНЫЙ ГОРКА 18:35 19:50

Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

1) 16:15 2) 18:15 3)18:30 4) 19:50

Решение («обратный ход»):

1) сначала заметим, что есть прямой рейс из аэропорта ВОСТОРГ в ГОРКУ с прибытием в 18:30:

ВОСТОРГ ГОРКА 16:15 18:30

2) посмотрим, сможет ли путешественник оказаться в ГОРКЕ раньше этого времени, если полетит через другой аэропорт, с пересадкой; рассмотрим все остальные рейсы, который прибывают в аэропорт ГОРКА:

ЗАРЯ ГОРКА 16:05 18:15

ОЗЕРНЫЙ ГОРКА 18:35 19:50

3) это значит, что имеет смысл проверить только возможность перелета через аэропорт ЗАРЯ (через ОЗЕРНЫЙ явно не получится раньше, чем прямым рейсом); для этого нужно быть в ЗАРЕ не позже, чем в 16:05

4) смотрим, какие рейсы прибывают в аэропорт ЗАРЯ раньше, чем в 16:05:

ОЗЕРНЫЙ ЗАРЯ 13:40 15:50

5) дальше проверяем рейсы, который приходят в ОЗЕРНЫЙ раньше, чем в 13:40

ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20

6) таким образом, мы «пришли» от конечного пункта к начальному, в обратном направлении

7) поэтому оптимальный маршрут

8) и правильный ответ – 2.

Возможные ловушки и проблемы: · «напрашивается» ошибочный ответ 18:30 (прямой рейс) · при решении задачи «прямым ходом», с начального пункта, легко пропустить вариант с двумя пересадками

[1] Крылов С.С., Ушаков Д.М. ЕГЭ 2010. Информатика. Тематическая рабочая тетрадь. — М.: Экзамен, 2010.