Понятие направленного угла между векторами вводится на ориентированной плоскости.
Пусть 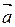 и
и 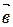 - ненулевые векторы, заданные в определенном порядке (
- ненулевые векторы, заданные в определенном порядке (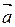 - первый вектор,
- первый вектор, 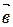 - второй вектор).
- второй вектор).
 Если
Если 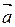 ||
|| 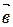 , то направленным углом между вектором
, то направленным углом между вектором 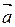 и вектором
и вектором 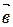 называется
называется
величина 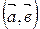 , если базис
, если базис 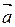 ,
, 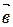 - правый;
- правый;
величина 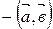 , если базис
, если базис 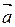 ,
, 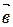 - левый.
- левый.
Если 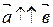 , то направленный угол между ними считается равным
, то направленный угол между ними считается равным 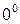 , если
, если 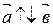 , то
, то 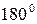 (рис. 43).
(рис. 43).
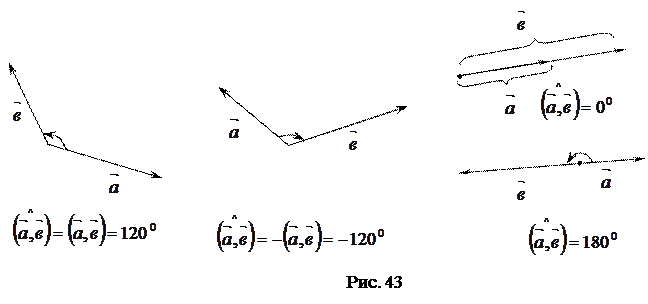 Направленный угол между вектором
Направленный угол между вектором 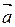 и вектором
и вектором 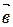 обозначается так:
обозначается так:
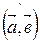 .
.
На чертеже направленный угол между векторами 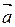 и
и 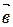 показывают дугой со стрелкой, идущей от первого вектора ко второму.
показывают дугой со стрелкой, идущей от первого вектора ко второму.
Из определения направленного угла между векторами 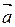 и
и 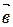 следует, что он находится в следующих пределах:
следует, что он находится в следующих пределах:
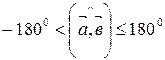 . .
|
Рассмотрим две прямоугольные декартовы системы координат 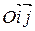 и
и 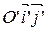 . Пусть М(х;у) в
. Пусть М(х;у) в 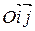 ,
, 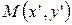 в
в 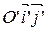 . Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты
. Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты 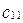 ,
, 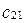 ,
, 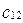 ,
, 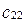 уже не могут быть произвольными.
уже не могут быть произвольными.
Найдем координаты векторов 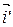 ,
, 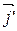 в старой системе
в старой системе 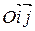 . Рассмотрим два случая.
. Рассмотрим два случая.
|
|
|
1) Базисы 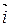 ,
, 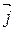 и
и 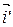 ,
, 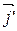 одинаково ориентированы (рис. 44).
одинаково ориентированы (рис. 44).
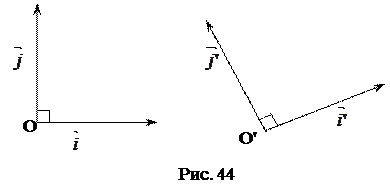
Пусть направленный угол 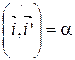 . Приведем векторы
. Приведем векторы 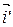 и
и 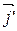 к общему началу О (рис. 45).
к общему началу О (рис. 45).
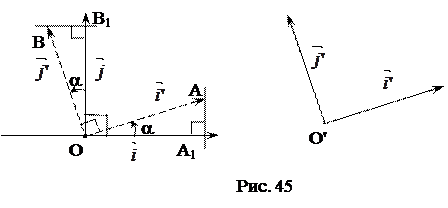 |
Прямоугольные треугольники 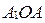 и
и 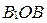 равны по гипотенузе и острому углу (
равны по гипотенузе и острому углу (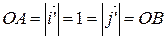 ,
, 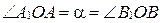 ), следовательно,
), следовательно, 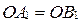 и
и 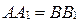 .
.
Из 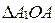 находим:
находим:
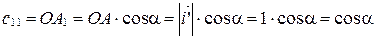 ;
;
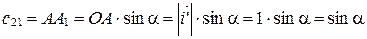 .
.
Следовательно, 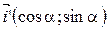 .
.
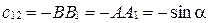 ;
; 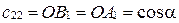 .
.
Следовательно, 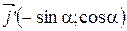 . Тогда формулы (5) примут вид:
. Тогда формулы (5) примут вид:
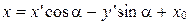 ;
;
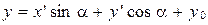 . (8)
. (8)
Заметим, что определитель матрицы перехода от базиса 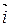 ,
, 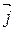 к базису
к базису 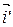 ,
, 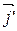
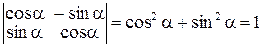 .
.
2) Базисы 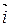 ,
, 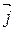 и
и 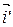 ,
, 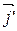 противоположно ориентированы (рис. 46).
противоположно ориентированы (рис. 46).
 Пусть
Пусть 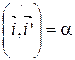 . Приведем векторы
. Приведем векторы 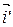 и
и 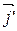 к общему началу О (рис. 47).
к общему началу О (рис. 47).
Рассуждая аналогично случаю 1), получим:
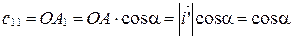 ;
;
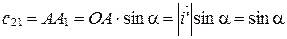 ;
;
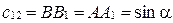 ;
; 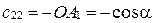 .
.
Следовательно, 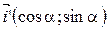 ;
; 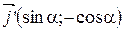 .
.
Тогда формулы (5) примут вид:
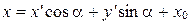 ;
;
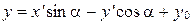 . (9)
. (9)
Заметим, что определитель матрицы перехода от базиса 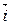 ,
, 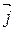 к базису
к базису 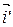 ,
, 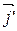 в этом случае
в этом случае
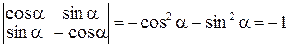 .
.
Формулы (8) и (9) можно объединить:
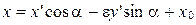 , ,
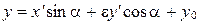 , ,
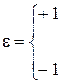
|
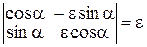 .
.
 2015-02-27
2015-02-27 450
450








