Одним из эффективных методов подсчёта вероятностей является формула полной вероятности, с помощью которой решается широкий круг задач.
Пусть событие A может наступить с одним и только одним из нескольких попарно несовместных событий Н 1, Н 2,…, Нn, называемых гипотезами, т.е.
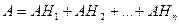 .
.
Так как Н 1, Н 2,… Нn попарно несовместны, то несовместны и события АН 1, АН 2,… АНn. Отсюда получаем, применяя формулы сложения и умножения вероятностей
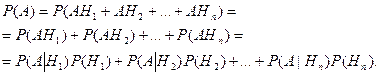
Полученная формула
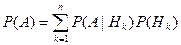 (1)
(1)
называется формулой полной вероятности.
Пример 1. (см. пример 1 §8). Из урны, в которой находятся m белых и n-m чёрных шаров, без возвращения выбираются два шара. Найдём вероятность события B ={второй вынутый шар – белый},
Рассмотрим гипотезы: H 1= {первый вынутый шар – белый) и 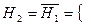 первый вынутый шар – чёрный}. Тогда
первый вынутый шар – чёрный}. Тогда 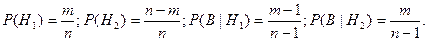 По формуле полной вероятности получаем
По формуле полной вероятности получаем 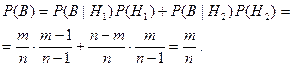
Таким образом, мы получим
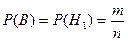 .
.
Аналогично можно установить, что вынимая последовательно без возвращения шары, мы получим одну и ту же вероятность вынуть белый шар на любом месте. Таким образом, при правильно организованной жеребьёвке, шансы всех участников одинаковы, независимо от того, в какой очерёдности они тянут жребий.
Замечание. Эту же задачу можно интерпретировать, как вычисление вероятности вытащить белый шар из урны, из которой был случайно утерян один или несколько шаров.
В тесной связи с формулой полной вероятности находятся так называемые формулы Байеса. Они относятся к той же ситуации, что и формула полной вероятности.
Поскольку событие А может наступить только вместе с одним из n попарно несовместных событий Н 1,… Нn , то найдём вероятность Р (Нк | А) – вероятность того, что событие А наступит вместе с гипотезой Нк.
По формуле умножения получаем 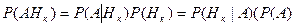
Откуда имеем
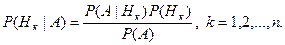 (2)
(2)
Или, если воспользоваться формулой полной вероятности (1) получим:

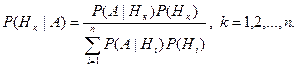 (3)
(3)
Это и есть формулы Байеса.
Запомнить эти формулы нетрудно: в знаменателе стоит выражение для полной вероятности, а в числителе – одно из слагаемых (к -ое) в этом выражении.
Формулы Байеса можно интерпретировать следующим образом.
Пусть A – результат некоторого эксперимента,
Нк – гипотезы. Вероятности Р(Нк) – это априорные вероятности гипотез, вычисленные до проведения опыта, а условные вероятности Р(Нк|А) – это апостериорные вероятности гипотез, вычисляемые после того, как стал известен исход эксперимента А. Формулы Байеса позволяют по априорным вероятностям гипотез и по условным вероятностям события А при гипотезах 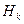 вычислять апостериорные вероятности Р(Нк|А).
вычислять апостериорные вероятности Р(Нк|А).
Пример 2. При обследовании больного имеется подозрение на одно из двух заболеваний Н 1 и Н 2. Их вероятности в данных условиях Р (Н 1)=0,6, Р (Н 2)=0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни Н 1 вероятность положительной реакции равна 0,9, отрицательной – 0,1. В случае Н 2 положительная и отрицательная реакции равновероятны. Анализ провели дважды, и оба раза реакция оказалась отрицательной (событие А). Требуется найти вероятности каждого заболевания после проделанных анализов.
Решение. В случае заболевания Н 1 событие А происходит с вероятностью 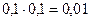 , а в случае заболевания Н 2 – с вероятностью
, а в случае заболевания Н 2 – с вероятностью 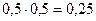 . Следовательно по формуле Байеса имеем
. Следовательно по формуле Байеса имеем 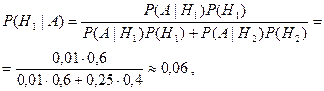 .
.
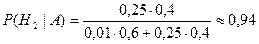 .
.
Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь Н 2.
 2015-02-27
2015-02-27 2037
2037








