Идея Робинсона – автора метода резолюций, - состоит в том, чтобы в логике предикатов можно было, работать, непосредственно, с дизъюнктами, содержащими переменные, не прибегая к предварительной замене переменных константами из области определения 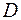 . Эта идея обеспечивается использованием операций подстановки и унификации. Чтобы определить суть этих операций, введем несколько новых понятий и определений.
. Эта идея обеспечивается использованием операций подстановки и унификации. Чтобы определить суть этих операций, введем несколько новых понятий и определений.
Понятие «выражение». Под выражением понимается терм, множество термов, множество атомов, литера, дизъюнкт, множество дизъюнктов. Когда в выражении не встречаются никакие переменные, оно называется основным выражением: основной атом, основная литера, основной дизъюнкт, основной терм, что говорит об отсутствии в них переменных.
Понятие «подстановка». Предварительно на примере выясним, в чем состоит проблема поиска контрарных пар в логике предикатов. Рассмотрим следующие дизъюнкты:

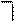
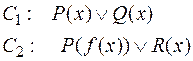
Пока нет никакой литеры в 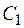 , контрарной какой-нибудь литере в
, контрарной какой-нибудь литере в 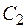 . Однако, подставив в
. Однако, подставив в 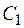 функцию
функцию 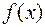 вместо переменной
вместо переменной 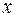 , получим:
, получим:
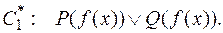
Теперь литера 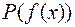 в
в 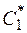 контрарна литере
контрарна литере 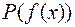 в
в 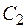 .
.
Следовательно, можно получить резольвенту из 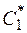 и
и 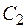 :
:
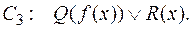
Определение 1: подстановка – это конечное множество вида 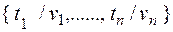 , где каждая
, где каждая 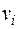 - это переменная, каждый
- это переменная, каждый 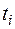 - терм, отличающийся от
- терм, отличающийся от 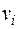 , а все
, а все 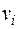 - различны.
- различны.
 Определение 2: Пусть
Определение 2: Пусть 
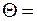
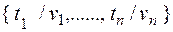 - подстановка, а - выражение. Тогда
- подстановка, а - выражение. Тогда 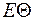 - это выражение, полученное из
- это выражение, полученное из 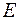 заменой одновременно всех вхождений переменной
заменой одновременно всех вхождений переменной 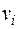
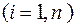 в выражении
в выражении 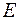 на терм
на терм 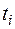 .
. 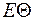 называется примером
называется примером 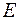 . Например, пусть
. Например, пусть 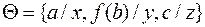 и
и 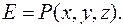 Тогда подстановка дает
Тогда подстановка дает 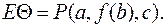
Понятие «композиция подстановок». Пусть даны подстановки 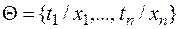 и
и 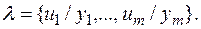 Тогда композиция
Тогда композиция 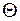 и
и 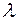 есть подстановка
есть подстановка 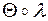 , которая получается из множества
, которая получается из множества 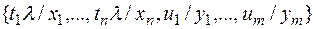 вычеркиванием всех элементов
вычеркиванием всех элементов 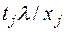 , для которых
, для которых 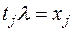 и всех элементов
и всех элементов 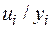 таких, что
таких, что 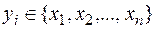 . Рассмотрим пример определения композиции подстановок
. Рассмотрим пример определения композиции подстановок 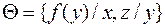 и
и 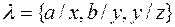 . Тогда
. Тогда 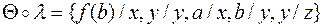 Однако по определению
Однако по определению 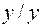 должна быть вычеркнута;
должна быть вычеркнута; 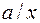 и
и 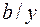 также должны быть вычеркнуты, так как
также должны быть вычеркнуты, так как 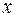 и
и 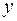 содержатся среди переменных подстановки
содержатся среди переменных подстановки 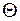 . В итоге получаем
. В итоге получаем 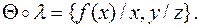
Понятие «унификатор для множества выражений». Подстановка 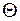 называется унификатором для множества выражений
называется унификатором для множества выражений 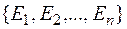 тогда и только тогда, когда
тогда и только тогда, когда 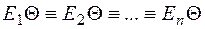 . Считается, что множество выражений унифицируемо, если для него существует унификатор.
. Считается, что множество выражений унифицируемо, если для него существует унификатор.
Унификатор 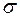 для множества выражений
для множества выражений 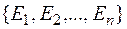 называется наиболее общим унификатором (НОУ) тогда и только тогда, когда для каждого унификатора
называется наиболее общим унификатором (НОУ) тогда и только тогда, когда для каждого унификатора 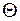 для этого множества существует токая подстановка
для этого множества существует токая подстановка 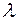 , что
, что 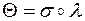 . Пусть, например, есть множество выражений
. Пусть, например, есть множество выражений 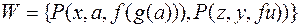 . Тогда
. Тогда 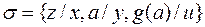 есть наиболее общий унификатор для
есть наиболее общий унификатор для 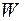 , а
, а 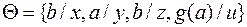 есть унификатор.
есть унификатор.
Опишем по шагам алгоритм унификации, который находит НОУ, если множество 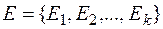 унифицируемо, и сообщает о неудаче, если это не так [ 6 ]:
унифицируемо, и сообщает о неудаче, если это не так [ 6 ]:
1) Установить 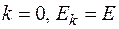 и
и 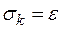 , где
, где 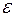 - пустая подстановка, не содержащая элементов. Перейти к шагу 2.
- пустая подстановка, не содержащая элементов. Перейти к шагу 2.
2) Если 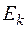 не является одноэлементным множеством, то перейти к шагу 3. В противном случае положить
не является одноэлементным множеством, то перейти к шагу 3. В противном случае положить 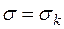 и окончить работу.
и окончить работу.
3) Каждая из литер в 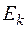 рассматривается как цепочка символов и выделяются первые подвыражения литер, не являющиеся одинаковыми у всех элементов
рассматривается как цепочка символов и выделяются первые подвыражения литер, не являющиеся одинаковыми у всех элементов 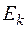 , т.е. образуется так называемое множество рассогласований типа
, т.е. образуется так называемое множество рассогласований типа 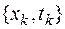 . Если в этом множестве
. Если в этом множестве 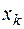 - переменная, а
- переменная, а 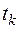 - терм, отличный от
- терм, отличный от 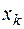 , то перейти к шагу 4. В противном случае окончить работу с выводом:
, то перейти к шагу 4. В противном случае окончить работу с выводом: 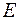 не унифицируемо.
не унифицируемо.
4) Пусть 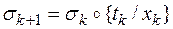 и
и 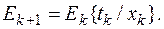
5) Установить 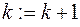 и перейти к шагу 2.
и перейти к шагу 2.
Рассмотрим работу алгоритма нахождения НОУ для множества 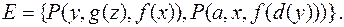 Шаги следующие:
Шаги следующие:
1) 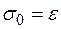 и
и 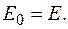
2) Так как 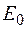 не является одноэлементным множеством, то перейти к шагу 3.
не является одноэлементным множеством, то перейти к шагу 3.
3) Множество рассогласований 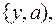 т.е. замена
т.е. замена 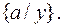
4) 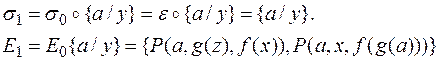
5) Так как множество 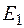 опять не одноэлементное, то множество рассогласований будет
опять не одноэлементное, то множество рассогласований будет 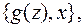 т.е. замена
т.е. замена 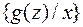 .
.
6) 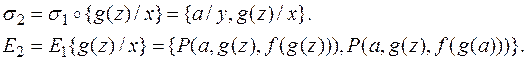
7) Имеем 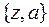 , т.е.
, т.е. 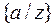 .
.
8) 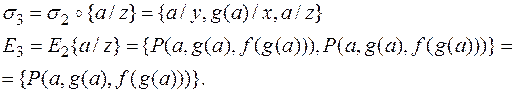
Так как получено одноэлементное множество, то искомый наиболее общий унификатор 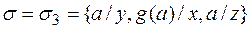 .
.
Можно показать, что алгоритм унификации всегда завершается на шаге 2, если множество 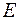 унифицируемо, и на шаге 3 - в противном случае.
унифицируемо, и на шаге 3 - в противном случае.
 Понятие «склейка дизъюнкта
Понятие «склейка дизъюнкта 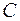 ». Если две или более литер (с одинаковым знаком) дизъюнкта
». Если две или более литер (с одинаковым знаком) дизъюнкта 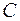 имеют наиболее общий унификатор
имеют наиболее общий унификатор 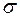 , то
, то 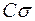 называется склейкой
называется склейкой 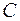 . Если
. Если 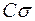 - единичный дизъюнкт, то склейка называется единичной склейкой.
- единичный дизъюнкт, то склейка называется единичной склейкой.
 Пример: Пусть
Пример: Пусть 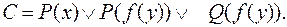
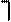 Тогда первая и вторая литеры имеют наиболее общий унификатор
Тогда первая и вторая литеры имеют наиболее общий унификатор 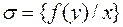 . Следовательно,
. Следовательно, 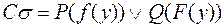 есть склейка
есть склейка 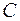 .
.
 Понятие «бинарная резольвента». Пусть
Понятие «бинарная резольвента». Пусть 
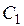 и
и 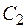 - два дизъюнкта (называемые дизъюнктами-посылками), которые не имеют никаких общих переменных. Пусть также
- два дизъюнкта (называемые дизъюнктами-посылками), которые не имеют никаких общих переменных. Пусть также 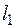 и
и 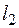 - две литеры соответственно в
- две литеры соответственно в 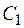 и
и 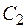 . Если
. Если 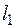 и
и 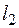 имеют наиболее общий унификатор
имеют наиболее общий унификатор 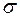 , то дизъюнкт
, то дизъюнкт 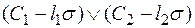 называется бинарной резольвентой
называется бинарной резольвентой 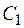 и
и 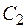 , а литеры
, а литеры 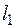 и
и 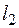 называются отрезаемыми литерами.
называются отрезаемыми литерами.
 Пример: Пусть
Пример: Пусть 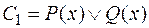 и
и 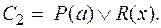 Так как переменная
Так как переменная 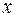 входит в
входит в 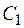 и
и 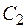 , то заменим переменную
, то заменим переменную 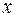 в
в 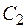 на
на 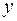 , т.е.
, т.е. 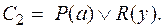 Выбираем
Выбираем 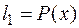 и
и 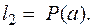 Так как
Так как 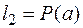 , то
, то 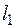 и
и 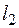 имеют наиболее общий унификатор
имеют наиболее общий унификатор 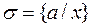 .
.


 Следовательно,
Следовательно,
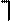
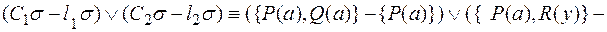

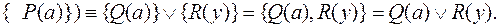
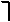 Таким образом,
Таким образом, 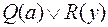 - бинарная резольвента
- бинарная резольвента 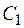 и
и 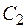 , а
, а 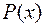 и
и 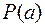 - отрезаемые литеры.
- отрезаемые литеры.
Понятие «резольвента логики первого порядка». Резольвентой дизъюнктов-посылок 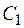 и
и 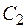 является одна из следующих резольвент:
является одна из следующих резольвент:
1) бинарная резольвента 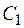 и
и 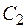 ;
;
2) бинарная резольвента 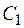 и склейки
и склейки 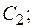
3) бинарная резольвента 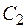 и склейки
и склейки 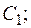
4) бинарная резольвента склейки 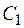 и склейки
и склейки 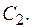
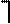 Пример: Пусть
Пример: Пусть 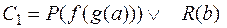 ,
,

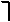
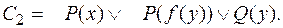

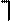 Тогда склейка дизъюнкта
Тогда склейка дизъюнкта 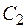 есть
есть 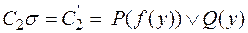 и резольвентой для
и резольвентой для 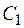 и
и 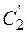 будет
будет 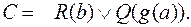 Вернуться
Вернуться
 2015-02-27
2015-02-27 1525
1525








