Примеры решения типовых задач. Пусть объект представлен структурной схемой, изображённой на рисунке 3.1

Задача 3.4.1.

Пусть объект представлен структурной схемой, изображённой на рисунке 3.1.

1. Составляем таблицу состояний (таблица 3.2), полагаем, что в каждом состоянии неисправен один из элементов:

S₁=S₁(0,1,1,1,1);

S₂=S₂(1,0,1,1,1);

S₃=S₃(1,1,0,1,1);

S₄=S₄(1,1,1,0,1);

S₅=S₅(1,1,1,1,0).

Таблица 3.2.

Si pk	S1	S2	S3	S4	S5	H(pk)	J(pk)
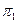
						1,6	0,72
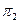
						1,36	0,96
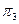
						2,32
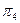
						1,6	0,72
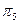
						1,36	0,96

2. По формуле 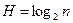вычисляем энтропию объекта перед началом поиска

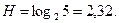
3. По формуле

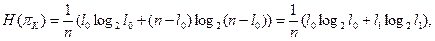
где l ₀, l ₁ – число нулей и число единиц в строке, соответствующей проверке p_k.

Находим энтропию объекта после проведения данной проверки (очередная условная энтропия вычисляется при условии, что проверка p_k проведена).

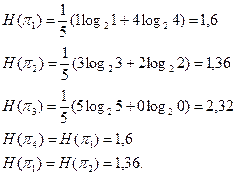
полученные данные заносим в столбец 7 таблицы 3.2.

4. По формуле J(p_k )=H-H(p_k) определяем количество информации, полученное при проведении p_k . Данные заносим в столбец 8 таблицы 3.2. Из таблицы видно, что максимальная информация получается при проведении проверок p₂ и p₅. Так проверка p₃ не несёт дополнительной информации её из дальнейшего рассмотрения исключаем.

5. Составляем таблицу 3.3., в которой в первой строке помещаем одну из проверок p₂ или p₅ (например p₂), а столбцы переставляем так, чтобы в строке соответствующей проверке p₂, стояли сначала нули, а затем единицы.

6. Заполним столбцы 7¸10 табл.3.3

Таблица 3.3

Si pk	S1	S2	S3	S4	S5	l00	l10	l01	l11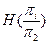
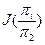
p1						-	-	-	-	-	-
p2										0,8	0,56
p3										0,8	0,56
p4										0,4	0,96

В ней:

l₀₀ – число нулей в p_i–й проверке, приходящихся на l₀ нулей в проверке p₂;

l₁₀ – число нулей в p_i–й проверке, приходящихся на l₀ нулей в проверке p₂;

l₀₁ – число нулей в p_i–й проверке, приходящихся на l₁ нулей в проверке p₂;

l₁₁– число нулей в p_i–й проверке, приходящихся на l₁ нулей в проверке p₂;

7. По формуле

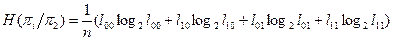
определяем среднюю энтропию объекта после проведения двух проверок в последовательности p₂®p_i.

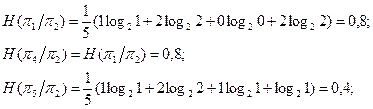
заполним столбец 11 в таблице 3.3

8. Определяем количество информации, получаемое при проведении проверки p_i/p₂(i=1,4,5),

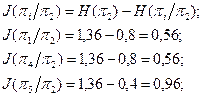
заполняем столбец 12 табл. 3.3.

Из таблицы следует, что в качестве второй проверки необходимо провести проверку p₅.

9. Составляем табл. 3.4., в которой первую строку оставляем для проверки p₂, вторую – для проверки p₅, вторую – для проверки p₅.

Таблица 3.4

Si pk	S1	S2	S3	S4	S5	l000	l100	l010	l110	l001	l101	l011	l111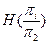
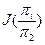
p1						-	-	-	-	-	-	-	-	-	-
p2						-	-	-	-	-	-	-	-	-	-
p3															0,4
p4														0,4

В таблице, например l₁₀₁ означает число единиц в проверке p _j, приходящихся на число нулей в проверке p₅, которая в свою очередь, приходятся на число единиц в проверке p₂.

10. По формуле

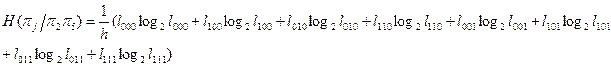
определяем энтропию объекта после проведения проверок в последовательности p₂®p₅®p _j

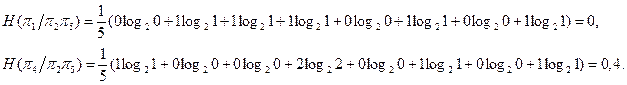11. Определяем количество информации, получаемое при проведении третьей проверки p _j (при условии, что проведены проверки p₂ и p₅ ):

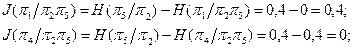
Заполняем графы 15 и 16 табл. 3.4.

Подводим окончательный итог: оптимальная последовательность проверок, обеспечивающая получение максимального количества информации и позволяющая однозначно диагностировать неисправность, будет следующей: p₂®p₅®p_1.

Задача 3.4.2.

Задача 3.4.3.

Пусть объект состоит из девяти элементов с известными вероятностями отказов:

q₁=0,1; q₂=0,15; q₃=q₄=0,25; q₅=q₆=q₇=0,03; q₈=0,15; q₉=0,01.

Время, требуемое для проверки, одинаково для всех элементов (t₁=t₂=...=t_n=const). Требуется определить последовательность проверок, обеспечивающую отыскание неисправности с наименьшими затратами времени.

Решение.

1. Располагаем элементы объекта в порядке убывания q_i: q₃=0,25; q₄=0,25; q₂=0,15; q₈=0,15; q₁=0,1; q₆=0,03; q₇=0,03; q₅=0,03; q₉=0,01.

2. Два элемента, имеющих наименьшую величину, в данном случае q₉= 0,01 и q₅=0,03, объединяем в один элемент, причём q=q₅+q₉=0,04.

3. Новый элемент по величине q(q₇=0,03)устанавливаем в имеющийся ряд элементов.

4. Повторяем пункты 1¸3 до тех пор, пока все элементы не объединятся в один.

Задача 3.4.4.

Система имеет интенсивность отказов l_0­=0,4×10^-5 1/ч. Её дублирует такая же система, находящаяся в режиме нагруженного резерва. Определить периодичность контроля, обеспечивающую снижение вероятности безотказной работы на величину, не превышающую D р=0,1.

Решение.

Для постоянного общего резервирования вероятность безотказной работы определим по формуле

,

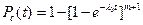для l₀t <<1 и m=1 имеем:

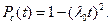
Учитывая, что заданное снижение вероятности безотказной работы D p=0,1, т.е. Р_тр(t)=0,9, получаем

Р_тр(t)=1-(l₀t_n)² ,

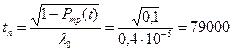(ч).

Задача 3.4.5.

В условиях предыдущей задачи определить, что повышает надёжность системы: изготовление её из высоконадёжных элементов, в результате чего интенсивность отказов снижается в 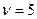раз, или применение нагруженного дублирования с контрольными проверками и восстановлением работоспособности через t_n=10ч.

Решение.

Пусть l₁– интенсивность отказов системы при изготовлении её из высоконадёжных элементов, l_р– интенсивность отказов дублированной системы.

Согласно условию

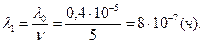
При нагруженном дублировании

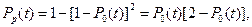
где

.

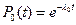Подставим выражение для P₀(t) в формулу для P_р(t), получаем

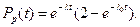
Интенсивность отказов резервированной системы равна

.

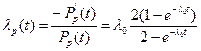При l₀t<<1 имеем приближенно

l_P(t)» 2 l²₀t.

Тогда среднее значение интенсивности отказов

.

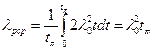Следовательно

.

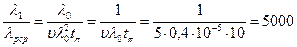Задача 3.4.6.

Имеются две аналогичные по характеристикам безотказности и восстанавливаемости системы, образующие схему постоянного дублирования. Каждая из них постоянно контролируются, причём, сразу же после отказа начинается восстановление. Определить коэффициент готовности системы.

Обозначим:

1- состояние системы, когда обе системы исправны;

2- состояние, когда один образец исправен, а второй ремонтируется;

3- состояние ремонта обоих образцов.

На рис.3.6. изображён граф переходов. Очевидно, что для рассматриваемой системы отказ определяется попаданием в состояние 3.

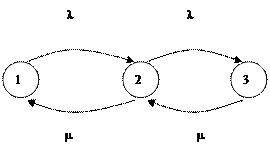Рис. 3.4

Для определения коэффициента готовности на основании мнемонического правила составим следующую систему:

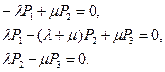
Второе уравнение является линейной комбинацией первого и третьего. Чтобы система была разрешима, в место второго уравнения добавим уравнение P₁+P₂+P₃=1. Тогда система примет вид:

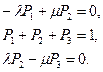
Решая эту систему, получим

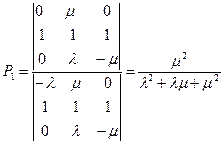
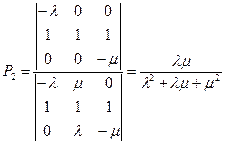
Отсюда

.

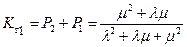при l=0,01 [1/ч], m=1,0 [1/ч], Кг=0,9999.

Если контроль отсутствует, то восстановление начинается после отказа двух систем. В этом случае можно ввести четыре состояния:

1- обе системы исправны;

2- одна система работает, вторая отказала, но не ремонтируется;

3- обе системы отказали и ремонтируются;

4- одна система работает, другая отказала и ремонтируется.

Подобная постановка задачи приводит к следующему графу переходов (рис.3.7.).

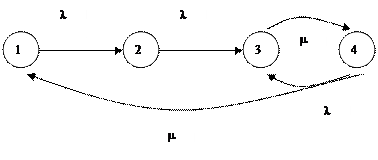На основании этого графа и вышеприведенного правила составляем следующее уравнения:

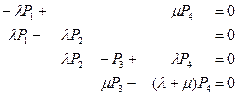
Исключить четвёртое уравнение и добавляя уравнение Р₁+Р₂+Р₃+Р₄=1, получаем следующее решение

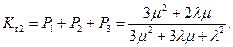
Для сравнения этих двух способов допустим, что

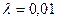1/ч и m=1,0 1/ч

Вычислим ожидаемый простой за 10000 часов эксплуатации. Так как

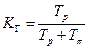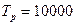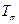, а – , то

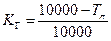=1-Т_п/10000 и Т_p=10000(1-К_г).

Для первого случая Т_п1 = 1 ч.

Для второго случая Т_п2 = 33 ч., т.е., если контроля нет, то ожидаемый простой за 10000 ч. эксплуатации составит 33 ч по сравнению с 1 ч., если имеется контроль.

Задачи

3.5.1. Составить таблицу состояний и определить последовательность проверок для объектов, заданных следующими функциональными моделями (рис.3.6).

3.5.2.

3.5.2–3.5.12. Определить последовательность проверок элементов системы для исходных данных, представленных в таблице 3.5.

Таблица 3.5.

№ задачи	Исходные данные
q1	q2	q3	q4	q5	q6	q7	q8	t1	t2	t3	t4	t5	t6	t7	t8
3.7.2	0,3	0,1	0,2	0,4	0,05	0,5	0,04	0,06
3.7.3	0,2	0,2	0,1	0,3	0,05	0,5	0,04	0,06
3.7.4	0,1	0,1	0,2	0,05	0,3	0,05	0,15	0,05
3.7.5	0,3	0,3	0,1	0,1	0,05	0,05	0,05	0,05
3.7.6	0,1	0,2	0,3	0,1	0,04	0,06	0,15	0,05
3.7.7	0,05	0,05	0,1	0,2	0,5	0,04	0,04	0,02
3.7.8	0,2	0,04	0,06	0,3	0,1	0,1	0,05	0,15
3.7.9	0,04	0,2	0,1	0,1	0,06	0,3	0,1	0,1
3.7.10	0,06	0,3	0,2	0,1	0,2	0,04	0,05	0,05
3.7.11	0,5	0,1	0,05	0,1	0,05	0,04	0,04	0,08
3.7.12	0,15	0,4	0,1	0,1	0,05	0,08	0,06	0,08

3.5.13. В условиях предыдущей задачи определить последовательность проверок элементов системы для случаев:

а) t₁=t₂=...=t_n=const.

б) q₁=q₂=...=q_n=const.

3.5.14–3.5.23. Определить периодичность контроля и дать сравнительную характеристику систем, представленных исходными данными в таблице. 3.6.

3.5.24.–3.7.33. Дать сравнительную характеристику нагруженных дублированных систем и систем с повышенной надёжностью элементов, для исходных данных, представленных в таблице 3.7.

3.5.34. Подсистема обработки данных АСУ построена по принципу «2 из 3», т.е. три идентичных подсистемы и решающий орган, выдающий на выходе правильный результат тогда, когда правильно функционируют хотя бы две из трёх подсистем. Интенсивность отказов каждой подсистемы равна l. Имеется ремонтный орган, который обеспечивает восстановление отказавшей подсистемы с интенсивностью восстановления, равной m. Определить коэффициент готовности подсистемы для двух случаев:

а) контроль отсутствует, и восстановление начинается только после отказа двух подсистем;

б) подсистема обработки данных постоянно контролируется.

3.5.35. В условиях предыдущей задачи определить коэффициент готовности для случаев:

а) 2 из 4; в) 3 из 4;

б) 2 из 5; г) 3 из 5.

Таблица 3.6

№ задачи	Исходные данные
l0 ´ 10 –3 1/4	m	D Р
3.5.14			0,1
3.5.15			0,2
3.5.16	1,5		0,1
3.5.17	1,6		0,15
3.5.18			0,15
3.5.19	2,8		0,1
3.5.20	1,7		0,1
3.5.21	0,5		0,15
3.5.22	1,2		0,2
3.5.23	1,4		0,2

Таблица 3.7

№ задачи	Исходные данные
	l0 ´ 10-4	tn
3.5.24
3.5.25
3.3.26
3.3.27
3.5.28		2,5
3.5.29		3,6
3.5.30		2,7
3.5.31		4,1
3.5.32		2,2
3.5.33

а)		б)
в)		г)
д)
е)
ж)
Рис. 3.6