2015-02-27
1444
Задачи оптимизации, в которых переменные должны быть целыми числами, называются задачами целочисленного (дискретного) программирования:
| Найти максимальное (минимальное) значение целевой функции | |
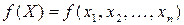 | (12.1) |
| при ограничениях | |
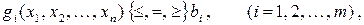 | (10.2) |
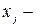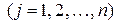 целые неотрицательные числа,  . | (10.3) |
Для получения целочисленных решений применяются специальные методы:
· методы отсечения;
· методы дерева решений;
· эвристические (приближенные) методы.
