2015-02-27
1253
В экономической деятельности часто возникают ситуации, в которых интересы сторон либо противоположны, либо не совпадают. При этом каждая сторона стремится получить наилучший результат за счет другой стороны. Это приводит к возникновению конфликтной ситуации. Теория игр занимается выработкой рекомендаций по оптимальному поведению сторон в конфликтной ситуации.
Исход игры – это значение некоторой функции, называемой функцией выигрыша (может задаваться аналитически или таблицей).
Рассмотрим таблицу решений, в которой строки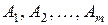 
соответствуют стратегиям 1-го игрока, а столбцы 
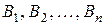– стратегии 2-го игрока. 
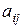– выигрыш (проигрыш), соответствующий каждой паре стратегий 
, 
.
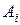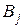| Стратегии 2-го игрока Стратегии 1-го игрока |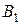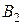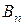 
| 
| … | 
|
| 
| 
| … | 
|
| 
| 
| … | 
|
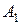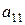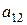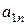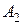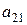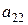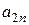| ¼ | … | … | … | … |
| 
| 
| … | 
|
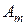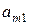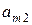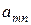Игра, в которой выигрыши и проигрыши игроков задаются матрицей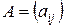 
, называется матричной игрой.
Стратегией в игре называется совокупность правил, определяющих выбор игроком одного из возможных вариантов действий.
|
|
|
Нижней ценой игры называется гарантированный выигрыш первого игрока (соответствующая стратегия называется максиминной)
.
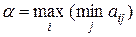Верхней ценой игры называется гарантированный проигрыш второго игрока (соответствующая стратегия называется минимаксной)
.
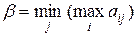Для матричных игр всегда справедливо неравенство
.
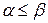Если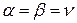 
, то игра называется игрой с седловой точкой. Элемент матрицы, соответствующий паре оптимальных стратегий, называется седловой точкой. Этот элемент называется ценой игры.
Если платежная матрица не имеет седловой точки, т.е.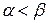 
, то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами.
