При моделировании, описание процессов исследуемого объекта сводится к составлению различного рода уравнений (алгебраических, дифференциальных интегральных), наиболее часто при решении задач используются следующие три вида уравнений:
1. дифференциальные уравнения в дифференциалах;
2. дифференциальные уравнения в производных;
3. простейшие интегральные уравнения с последующим преобразованием их в дифференциальные уравнения.
Рассмотрим, как составляются уравнения каждого из приведенных видов.
Уравнения в дифференциалах. Сущность метода дифференциалов заключается в том, что из условия задач составляются соотношения между дифференциалами. Для этого малые приращения величин заменяются их дифференциалами, неравномерно протекающие физические процессы в течение малого промежутка времени 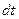 рассматриваются как равномерные. Так как отношение дифференциалов функции и аргумента является пределом отношения их приращений, то по мере того, как приращения стремятся к нулю, принятые допущения выполняются с большой точностью. Получающиеся при этом дифференциальные уравнения оказываются точными, если они однородны и линейны относительно дифференциалов.
рассматриваются как равномерные. Так как отношение дифференциалов функции и аргумента является пределом отношения их приращений, то по мере того, как приращения стремятся к нулю, принятые допущения выполняются с большой точностью. Получающиеся при этом дифференциальные уравнения оказываются точными, если они однородны и линейны относительно дифференциалов.
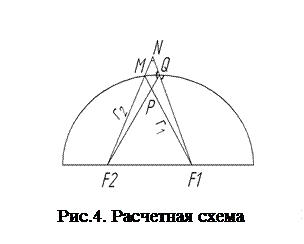
Пусть перед исследователем стоит задача определения поверхности вращения, по которой нужно отшлифовать зеркало рефлектора, чтобы выходящие из одной точки световые лучи после отражения в зеркале пересекались в другой точке.
Задача сводится к нахождению уравнения сечения искомой поверхности меридианной плоскостью, проходящей через точку 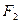 , в которой помещается источник света, и точку
, в которой помещается источник света, и точку 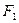 , в которой пересекаются отраженные лучи (рис.4).
, в которой пересекаются отраженные лучи (рис.4).
Пусть 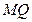 – малая дуга этого сечения. Будем ее считать прямолинейным отрезком. Опишем из точек
– малая дуга этого сечения. Будем ее считать прямолинейным отрезком. Опишем из точек 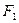 и
и 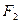 , как из центров, дуги MN и MP окружностей радиусами
, как из центров, дуги MN и MP окружностей радиусами 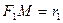 и
и 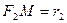 . Эти дуги также будем считать прямолинейными отрезками.
. Эти дуги также будем считать прямолинейными отрезками.
 Треугольники
Треугольники 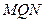 и
и 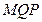 – прямоугольные (
– прямоугольные (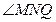 и
и 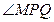 – прямые) с общей гипотенузой
– прямые) с общей гипотенузой 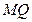 .
.
Пользуясь известным законом оптики о равенстве углов падения и отражения, а также свойством равенства вертикальных углов, находим, что 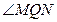 =
= 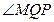 и
и 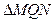 =
= 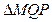 . Отсюда следует, что
. Отсюда следует, что 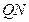 =
= 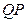 . Так как
. Так как 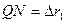 , а
, а 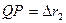 , то, заменяя приращения радиусов-векторов
, то, заменяя приращения радиусов-векторов 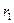 и
и 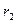 их дифференциалами, имеем дифференциальное уравнение
их дифференциалами, имеем дифференциальное уравнение
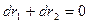 или
или 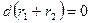
откуда находим общий интеграл
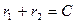 .
.
Сечение искомой поверхности меридианной плоскостью является эллипсом. Следовательно, зеркало рефлектора необходимо отшлифовать по поверхности эллипсоида вращения.
Уравнения в производных. Сущность метода производных заключается в том, что из условия задачи составляются приближенные соотношения между скоростями изменения функции и аргумента.
Например, при исследовании роста числа публикаций в науке исходят из выявленной закономерности, что скорость роста 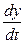 пропорциональна достигнутому уровню y числа публикаций.
пропорциональна достигнутому уровню y числа публикаций.
Следовательно, дифференциальное уравнение примет вид
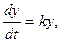
где k = const, относительная скорость роста числа публикаций.
Решение этого дифференциального уравнения имеет вид
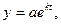
где a – постоянная, характеризующая некоторое начальное число публикаций.
3. Простейшие интегральные уравнения. При рассмотрении работы сил, объемов тел, площадей криволинейных поверхностей их можно описать при помощи определенного интеграла или интегральных формул. В случае если при таком описании неизвестные функции попадают под знак интеграла, то получаемая формальная запись называется интегральным уравнением.
Последующее дифференцирование интегрального уравнения преобразует его в дифференциальное.
Например, пусть нужно найти закон прямолинейного движения материальной точки массы m, если известно, что работа действующей на точку силы пропорциональна времени t, прошедшему от начала движения. Начальный путь и начальная скорость равны соответственно s0 и v0.
Из курса механики известно, что в случае прямолинейного перемещения точки, когда направления силы и скорости совпадают, работа 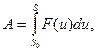 где F(u) – действующая на точку сила.
где F(u) – действующая на точку сила.
По условию задачи
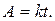
Сравнивая оба выражения для А, находим
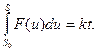
Дифференцированием по s получаем
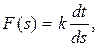
а так как 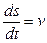 – скорость движения и
– скорость движения и
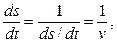
то
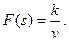
Из второго закона Ньютона следует, что
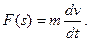
Сравнивая оба выражения для F(s), составляем дифференциальное уравнение
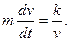
Общее решение этого уравнения представляется в виде
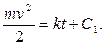
При начальном условии v = v0 при t = 0 находим, что

Следовательно,
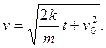
Заменяя v на 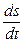 и интегрируя, находим
и интегрируя, находим
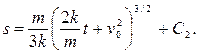
При t = 0 s = s0, следовательно,
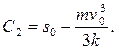
Таким образом, закон движения материальной точки принимает вид
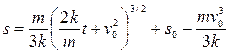 .
.
 2015-02-04
2015-02-04 1143
1143








