Дайте определение градиента

Под градиентом скалярной функции понимают скорость изменения скалярной функции, взятой в направлении ее наибольшего возрастания. При этом в декартовой системе координат

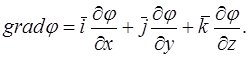(23.2)

Для сокращения записей различных операций над скалярными и векторными величинами употребляется дифференциальный оператор Гамильтона (оператор набла)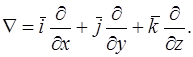

Другими словами, запись Ñ j эквивалентна записи grad j, а “приписывание” слева к какой-либо скалярной функции (в нашем случае к j) оператора Ñ означает взятие градиента от этой скалярной функции.

Подставим в уравнение Гаусса 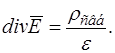уравнение (23.1). Получим 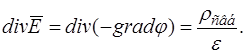или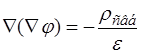

или 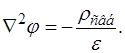(23.3)

Уравнение (23.3) называется уравнением Пуассона. Частный вид уравнения Пуассона, когда r _свб = 0, называется уравнением Лапласа. Уравнение Лапласа запишется так Ѳ j = 0, (23.4)

Оператор Ѳ = div grad называют оператором Лапласа или лапласианом. В декартовой системе координат он равен 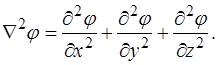Тогда уравнение Пуассона в декартовой системе координат запишется следующим образом:

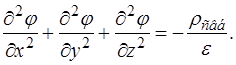(23.5)