| Действие магнитного поля на проводник с током Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. | |
| Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B.I.ℓ. sin α — закон Ампера. | 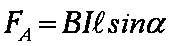 |
| Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током. | 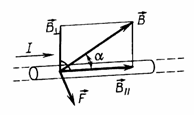 |
23. Дипольный магнитный момент;
Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являютсяэлектрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток). Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.
Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10−3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора.
Формулы для вычисления магнитного момента
В случае плоского контура с электрическим током магнитный момент вычисляется как
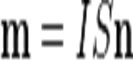 ,
,
где 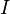 — сила тока в контуре,
— сила тока в контуре, 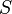 — площадь контура,
— площадь контура, 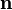 — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.
Для произвольного замкнутого контура магнитный момент находится из:
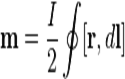 ,
,
где 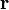 — радиус-вектор, проведенный из начала координат до элемента длины контура
— радиус-вектор, проведенный из начала координат до элемента длины контура 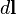
В общем случае произвольного распределения токов в среде:
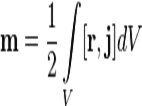
где 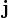 — плотность тока в элементе объёма
— плотность тока в элементе объёма 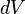 .
.
24. Теоремы о потоке и циркуляции вектора магнитной индукции;
Циркуляцией вектора индукции магнитного поля (циркуляцией вектора 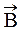 ) называют криволинейный интеграл по произвольному контуру L скалярного произведения вектора индукции
) называют криволинейный интеграл по произвольному контуру L скалярного произведения вектора индукции 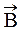 и вектора элемента этого контура
и вектора элемента этого контура 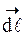 , т. е.
, т. е.
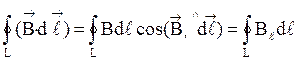 , (25)
, (25)
где 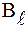 - проекция
- проекция 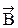 на
на 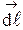 .
.
Циркуляция 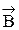 по произвольному контуру L в вакууме равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охваченных этим контуром.
по произвольному контуру L в вакууме равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охваченных этим контуром.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта, а ток противоположного направления - отрицательным (рис. 7, где I1 > 0, I3 > 0, I2 < 0, I4 < 0).
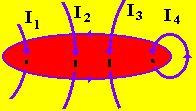 Рис.7. Рис.7. |
Рассмотрим магнитное поле прямого проводника с током бесконечной длины (рис.8, ток направлен к нам). В качестве замкнутой поверхности используем окружность L радиуса r. Вектор индукции магнитного поля 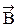 перпендикулярен радиус-вектору
перпендикулярен радиус-вектору 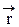 и совпадает по направлению с вектором элемента длины
и совпадает по направлению с вектором элемента длины 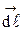 .
.
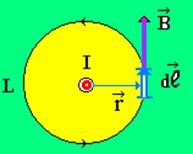 Рис. 8 Рис. 8 |
Согласно определению циркуляции вектора 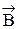 имеем
имеем
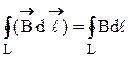 , (cosa =1).
, (cosa =1).
Применив формулу индукции прямого проводника с током бесконечной длины, последнее равенство перепишем в виде
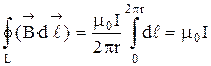 . (26)
. (26)
Теорема остается справедливой и для контура произвольной формы, который охватывает N проводников с током, т. е.
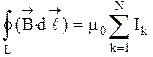 . (27)
. (27)
Формулу (27) называют законом полного тока.
Если ток распределен по объему, где расположен контур L, то
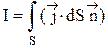 .
.
Интеграл берется по произвольной поверхности S, натянутой на контур L.
Поэтому плотность тока 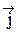 под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали
под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали 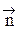 связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде
связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде
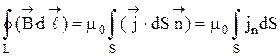 . (28)
. (28)
Дифференциальная форма теоремы о циркуляции 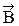
Рассмотрим отношение циркуляции вектора 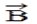 к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали
к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали 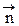 к плоскости контура правилом правого винта. В пределе при S ® 0, имеем
к плоскости контура правилом правого винта. В пределе при S ® 0, имеем
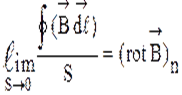 . (29)
. (29)
Формулу (29) называют ротором поля 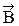 .
.
Следовательно, этот предел представляет собой скалярную величину, равную проекции вектора 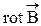 на нормаль. Используя (29), формулу (28) представим в виде
на нормаль. Используя (29), формулу (28) представим в виде
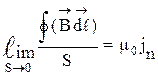 (30)
(30)
или
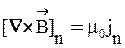 , (31)
, (31)
где 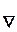 - векторный дифференциальный оператор.
- векторный дифференциальный оператор.
Следовательно,
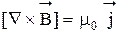 . (32)
. (32)
Ротор поля 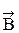 совпадает по направлению с вектором плотности тока
совпадает по направлению с вектором плотности тока 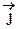 в данной точке. Формула (32) - дифференциальная форма теоремы о циркуляции
в данной точке. Формула (32) - дифференциальная форма теоремы о циркуляции 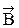 . Дифференциальная форма теоремы о циркуляции
. Дифференциальная форма теоремы о циркуляции 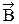 расширяет ее возможности для исследования и расчета сложных магнитных полей.
расширяет ее возможности для исследования и расчета сложных магнитных полей.
25. Вектор намагниченности;
Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёмавещества:
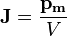
Здесь, J — вектор намагниченности; 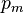 — вектор магнитного момента; V — объём.
— вектор магнитного момента; V — объём.
В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как
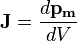
и является функцией координат. Где 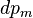 есть суммарный магнитный момент молекул в объеме dV Связь между J и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):
есть суммарный магнитный момент молекул в объеме dV Связь между J и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):
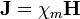
где χ m называют магнитной восприимчивостью. В ферромагнитных материалах нет однозначной связи между J и H из-за магнитного гистерезиса и чтобы описать зависимость используют тензор магнитной восприимчивости.
Магнитная индукция определяется через намагниченность как:
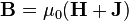 (в системе СИ)
(в системе СИ)
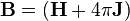 (в системе СГС)
(в системе СГС)
 2015-02-04
2015-02-04 1164
1164
