2015-06-04
18885
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
1.1. Криволинейный интеграл 1 рода.
1.1.1. Определение криволинейного интеграла 1 рода
Пусть на плоскости Оxy задана кривая (L). Пусть для любой точки кривой (L) определена непрерывная функция f(x;y). Разобьем дугу АВ линии (L) точками А=P0, P1 , Pn = В на n произвольных дуг Pi-1 Pi с длинами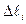 
(i = 1, 2, n) (рис.27)
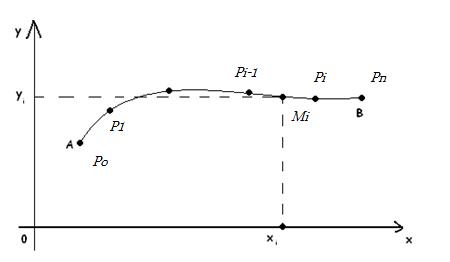
Рис.27
Выберем на каждой дуге Pi-1 Pi произвольную точку Mi (xi; yi), вычислим значение функции f(x;y) в точке Mi. Составим интегральную сумму
.
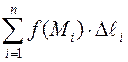Пусть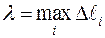 
, где 
.
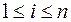Если существует предел интегральной суммы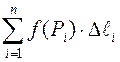 
при λ→0 (n→∞), не зависящий ни от способа разбиения кривой (L)на элементарные части, ни от выбора точек Mi в каждой элементарной части, то этот предел называют криволинейным интегралом 1 рода от функции f(x;y) (криволинейным интегралом по длине дуги) и обозначают:
.
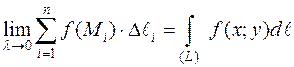Замечание. Аналогично вводиться определение криволинейного интеграла от функции f(x;y;z) по пространственной кривой (L).
Физический смысл криволинейного интеграла 1 рода:
Если (L)- плоская кривая с линейной плоскостью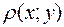 
, то массу кривой находят по формуле:
.
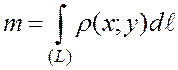1.1.2. Основные свойства криволинейного интеграла 1 рода:
1. 
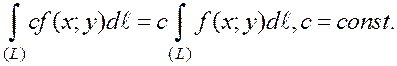
2. 
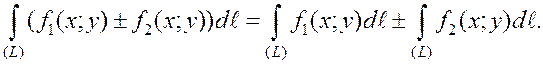
3. Если путь интегрирования разбит на части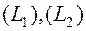 
такие что 
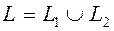, и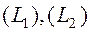 
имеют единственную общую точку, то 
.
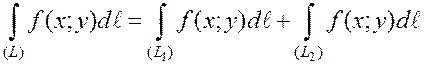4. Криволинейный интеграл 1 рода не зависит от направления интегрирования:
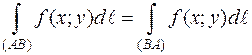
5. 
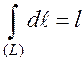, где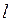 
- длина кривой.
1.1.3. Вычисление криволинейного интеграла 1 рода.
Вычисление криволинейного интеграла сводят к вычислению определенного интеграла.
1. Пусть кривая (L) задана уравнением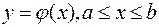 
. Тогда
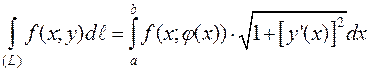, то есть дифференциал дуги вычисляют по формуле 
.
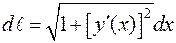Пример
Вычислить массу отрезка прямой от точки А(1;1) до точки В(2;4), если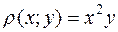 
.
Решение
Уравнение прямой проходящей через две точки: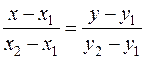 
.
Тогда уравнение прямой (АВ):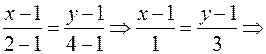 
, 
.
; 
, .
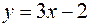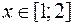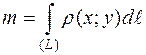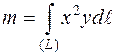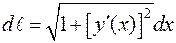Найдём производную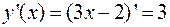 
.
Тогда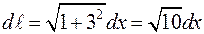 
. 
= 
.
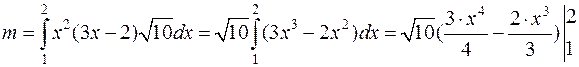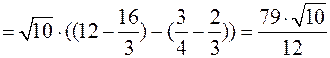2. Пусть кривая (L) задана параметрически: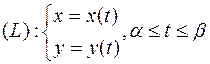 
.
Тогда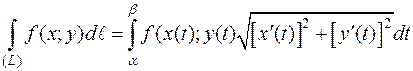 
, то есть дифференциал дуги вычисляют по формуле 
.
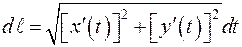Для пространственного случая задания кривой: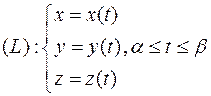 
.Тогда
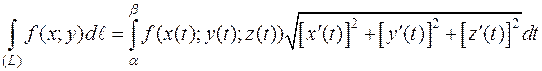,то есть дифференциал дуги вычисляют по формуле 
.
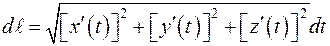Пример
Найти длину дуги кривой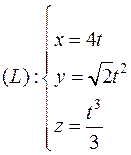 
, 
.
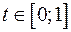Решение
Длину дуги найдём по формуле: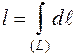 
.
Для этого найдём дифференциал дуги .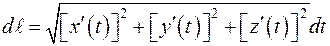
Найдём производные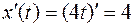 
, 
, 
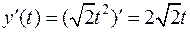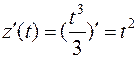.Тогда 
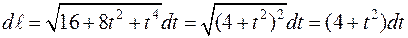и длина дуги: 
.
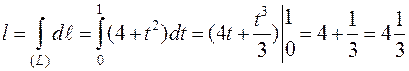3. Пусть кривая (L) задана в полярной системе координат: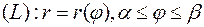 
. Тогда
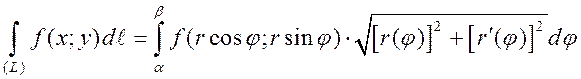, то есть дифференциал дуги вычислют по формуле 
.
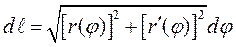Пример
Вычислить массу дуги линии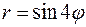 
, 0≤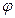 
≤ 
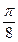, если 
.
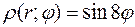Решение
Массу дуги найдём по формуле:
.
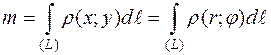Для этого найдёмдифференциал дуги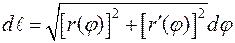 
.
Найдём производную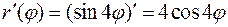 
.
.
= 
=
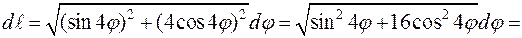
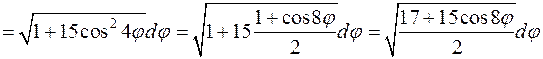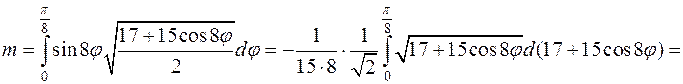
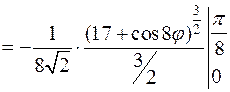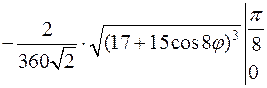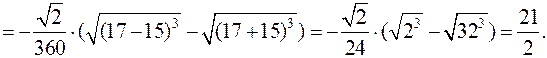
1.2. Криволинейный интеграл 2 рода
1.2.1. Определение криволинейного интеграла 2 рода
Пусть на плоскости Оxy задана кривая (L). Пусть на (L) задана непрерывная функция f (x;y). Разобьем дугу АВ линии (L) точками А = P0 ,P1 , Pn = В в направлении от точки А к точке В на n произвольных дуг Pi-1 Pi с длинами 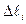(i = 1, 2, n) (рис.28).
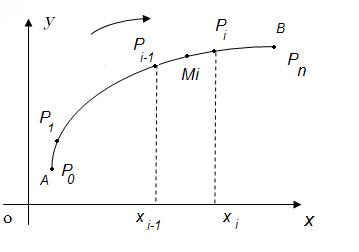
Рис.28
Выберем на каждой дуге Pi-1Pi произвольную точку Mi (xi; yi), вычислим значение функции f(x;y) в точке Mi. Составим интегральную сумму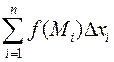 
, где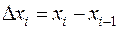 
- длина проекции дуги Pi-1Pi на ось Оx. Если направление движения вдоль проекции совпадает с положительным направлением оси Оx, то проекцию дуг считают положительной, иначе - отрицательной.
Пусть 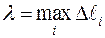, где .
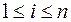Если существует предел интегральной суммы 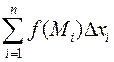при λ→0 (n→∞), не зависящий ни от способа разбиения кривой (L) на элементарные части, ни от выбора точек Mi в каждой элементарной части, то этот предел называют криволинейным интегралом 2 рода от функции f(x;y) (криволинейным интегралом по координате х) и обозначают:
.
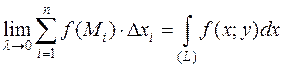Замечание. Аналогично вводится криволинейный интеграл по координате у:
.
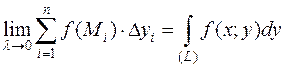Замечание. Если (L) - замкнутая кривая, то интеграл по ней обозначают
.
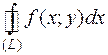Замечание. Если на (L) задано сразу три функции и от этих функций существуют интегралы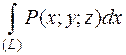 
, 
, 
,
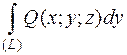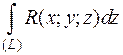то выражение: 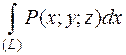+ + 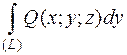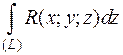называют общим криволинейным интегралом 2 рода и записывают:
+ 
+ 
.
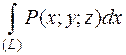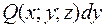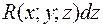1.2.2. Основные свойства криволинейного интеграла 2 рода:
1. 
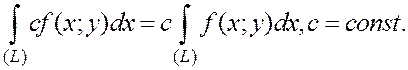
2. 
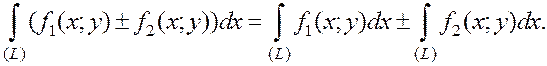
3. При изменении направления интегрирования криволинейный интеграл 2 рода изменяет свой знак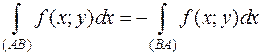 
.
4. Если путь интегрирования разбит на части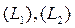 
такие что 
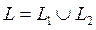, и 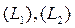имеют единственную общую точку, то
= 
+ 
.
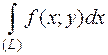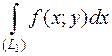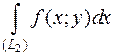5. Если кривая (L) лежит в плоскости:
- перпендикулярной оси Ох, то 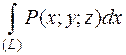=0;
- перпендикулярной оси Oy, то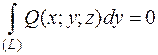 
;
- перпендикулярной оси Oz, то 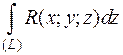=0.
6. Криволинейный интеграл 2 рода по замкнутой кривой не зависит от выбора начальной точки (зависит только от направления обхода кривой).
1.2.3. Физический смысл криволинейного интеграла 2 рода.
Работа А силы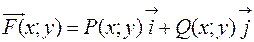 
при перемещении материальной точки единичной массы из точки М в точку N вдоль (MN) равна:
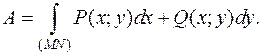
1.2.4. Вычисление криволинейного интеграла 2 рода.
Вычисление криволинейного интеграла 2 рода сводят к вычислению определенного интеграла.
1. Пусть кривая (L) задана уравнением .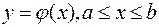
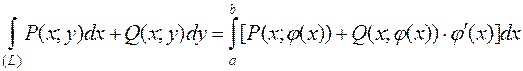, где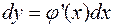 
.
Пример
Вычислить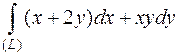 
, где (L)- ломаная OAB: O(0;0), A(0;2), B(2;4).
Решение
Так как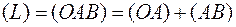 
(рис.29), то
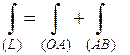
1)Уравнение (OA):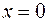 
, 
,
.
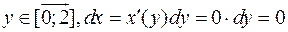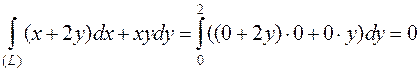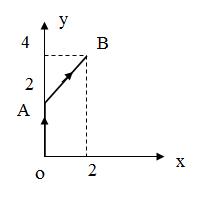
Рис.29
2) Уравнение прямой (AB):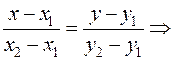 
.
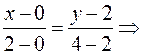
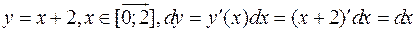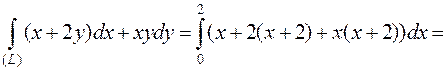
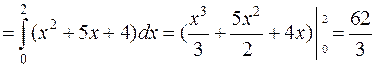
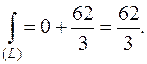
2. Пусть кривая (L) задана параметрически: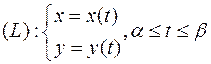 
.
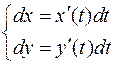.Тогда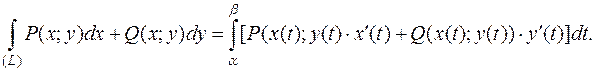 
Замечание. В пространственном случае:
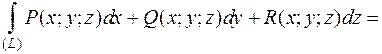
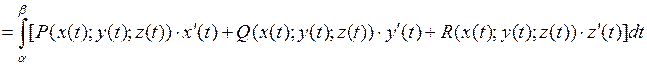Пример
Вычислить
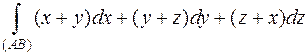,где (АВ)- отрезок от А(0;0;1) до B(2;-2;3).
Решение
Найдём уравнение прямой (АВ):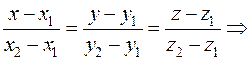 
.
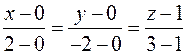Перейдём к параметрической записи уравнения прямой (АВ)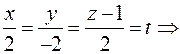 
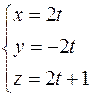. Тогда 
.
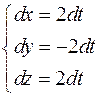Точке A(0;0;1) соответствует параметр t равный: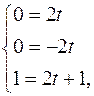 
следовательно, t=0.
Точке B(2;-2;3) соответствует параметр t, равный: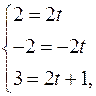 
следовательно, t=1.
При перемещении от А к В 
,параметр t меняется от 0 до 1 
.
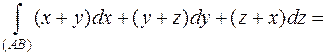
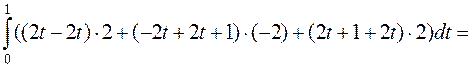
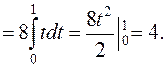
1.3. Формула Грина
Формула связи двойного интеграла по плоской области (D) и криволинейного интеграла по границе (L) этой области (рис.30).
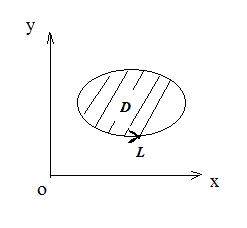
Рис.30
Теорема. Если функци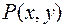и 
и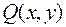 
непрерывны вместе со своими частными производными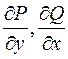 
в области (D), то имеет место формула:
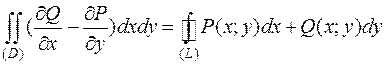- формула Грина,
где (L) - граница области (D). Интегрирование ведётся в положительном направлении (при обходе (L)область остаётся слева).
Пример
Вычислить интеграл по замкнутому контуру по формуле Грина:
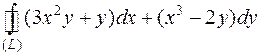, где (L): 
.
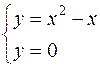Решение
Построим контур интегрирования (рис.31). Для этого найдем точки пересечения параболы с осью Оx и координаты вершины параболы 
.
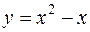Точки пересечения с осью Оx: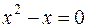 
, 
, 
.
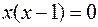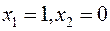Координаты вершины параболы: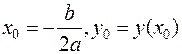 
.
.
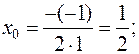
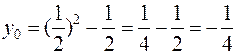Вершина параболы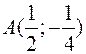 
.
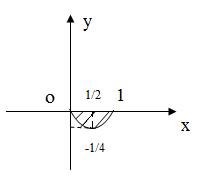
Рис.31
Очевидно, что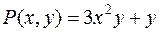 
, 
, 
.
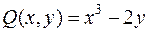
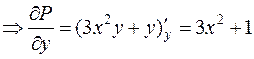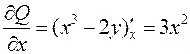Применим формулу Грина:
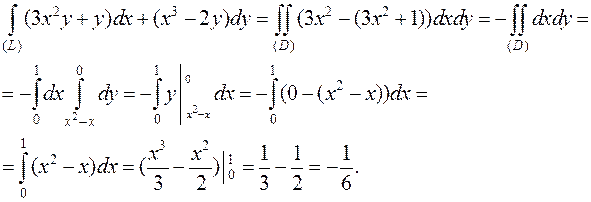
1.4. Условие независимости криволинейного интеграла 2 рода от пути интегрирования.
Теорема. Для того, чтобы криволинейный интеграл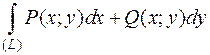 
не зависел от пути интегрирования в односвязной области (D), в которой функци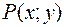и 
и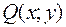 
непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке области выполнялось равенство:
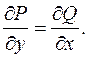
Пример
Вычислить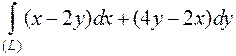 
, где (L) отрезок от точки А(1;1) до В(2;8).
Решение
Очевидно, что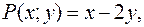 
.
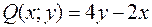Тогда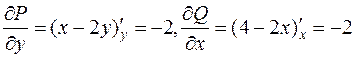 
.То есть 
.
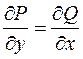Следовательно, в качестве пути интегрирования можно взять например отрезок кривой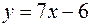 
или дугу 
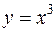(уравнениям этих линий удовлетворяют координаты точек А и В).
1. 
, 
.
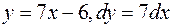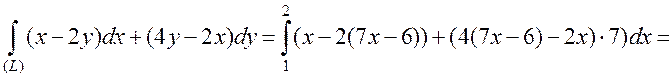
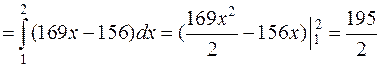2. 
, 
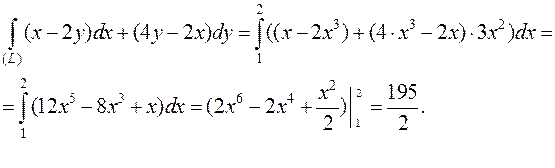
1.5. Формула связи между криволинейными интегралами 1 и 2 рода.
Криволинейные интегралы 1 и 2 рода связаны формулой:
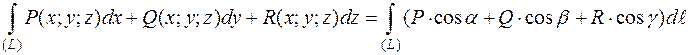Где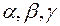 
- углы, образованные касательной к кривой (L) в т. М(х;у;z) с осями Оx, Оy, Oz
