Критерий Абсолютной устойчивости нелинейных систем В.М. Попова, его применение

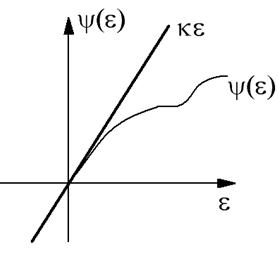
Под абсолютной устойчивостью нелинейной системы понимают ее устойчивость при любых начальных условиях и любой форме нелинейности, принадлежащей Гурвицеву углу. Т.е. система будет абсолютно устойчивой, если она устойчива при любой нелинейной характеристике ψ(ε), укладывающейся в определённый, так называемый, Гурвицев угол.

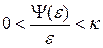
Иногда вместо 0 ставят начальные условия.

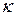- заданное число.

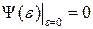- проходит через начало координат.

На основании этого был сформулирован критерий абсолютной устойчивости В.М. Попова.

Метод Попова является частотным, основанный на следующем.

Система, описанная нелинейным уравнением в отклонениях:

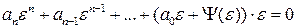
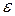– отклонение координаты от заданных значений.

Если в нём нелинейную функцию заменить на линейную зависимость:

;

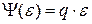где q – любое число, удовлетворяет неравенству 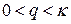, то если после замены нелинейной функции линейной зависимостью получим характеристическое уравнение, отвечающее требованию устойчивости, то и нелинейная система будет устойчива.

Если известна ЛАЧХ линейной части системы (линейная часть должна быть устойчива) и задано значение параметра 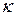, то для исследования устойчивости необходимо записать функцию Попова:

;

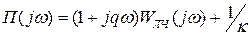где q – постоянное число, характеризующее нелинейность.

Раскроем скобки, тогда:

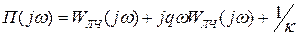
Система будет абсолютно устойчивой, если можно подобрать такое вещественное число q, при котором в диапазоне частот (0;∞) будет выполняться условие:

; ;

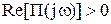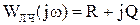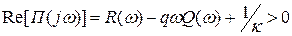
Это уравнение можно привести к виду:

; ;

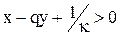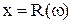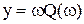
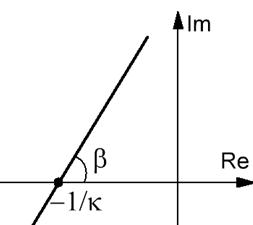
Если неравенство заменить равенством, то получим границу устойчивости. Граница устойчивости – линия проходящая через точку на действительной оси с абсциссой 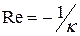и угловым коэффициентом .

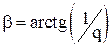Этот критерий имеет удобную геометрическую трактовку.

Формулировка: НС будет абсолютно устойчивой, если в плоскости видоизменённой частотной характеристики линейной части системы 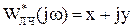, можно провести через точку с координатой 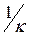любую наклонную прямую так, что бы видоизменённая линейная характеристика части системы лежала справа от этой прямой.

;

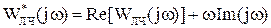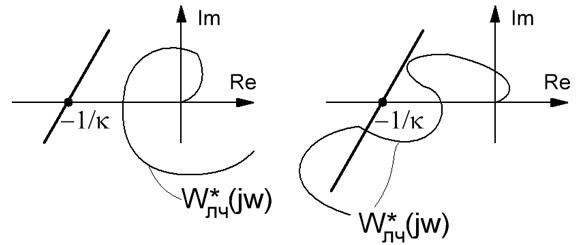
Абсолютно устойчива Абсолютно неустойчива

Если такую прямую провести не удаётся, то нет условия абсолютной устойчивости системы при рассмотренных параметрах.