В) Устойчивость линейных активных цепей с обратной связью

Физический смысл понятия “устойчивая работа активной цепи” состоит в том, что устойчивая цепь после прекращения действия внешних возмущений возвращается в исходное состояние. В противном случае любое внешнее возмущение приводит к развивающимся во времени колебательным процессам вплоть до генерации. Следовательно, в устойчивой активной цепи переходные процессы должны быть затухающими.

Возможны, по крайней мере, два пути анализа устойчивости:

- исследование переходного процесса замкнутой цепи

- исследование частотной зависимости петлевого коэффициента усиления цепи обратной связи.

Первый путь приводит к, так называемому, алгебраическому критерию устойчивости, второй - к частотному. Очевидно, что оба метода взаимосвязанны.

1. Алгебраический критерий устойчивости.

Из теории электрических цепей известно, что напряжения или токи на входе и выходе произвольной линейной цепи связаны между собой дифференциальным уравнением

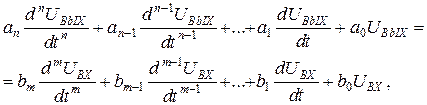(48)

где m,n - целые числа, определяющие порядок уравнения (или порядок цепи);

a_n, b_m - постоянные вещественные числа.

Пример цепи первого порядка - RC — ФНЧ и RC — ФВЧ.

Проблема устойчивости сводится к анализу зависимости выходного напряжения от времени при U_BX. В этом случае анализируют только собственные колебания, то есть колебания, которые принципиально могут существовать в цепи. Но это не означает, что они обязательно возникают в реальной цепи при U_BX¹0.

Полагая в (48) U_BX=0, получим однородное дифференциальное уравнение, решением которого являются собственные колебания цепи:

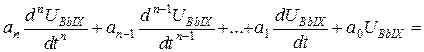0 (49)

Решением (49) являются функции вида e^Pit, где p_i - корни характеристического уравнения вида

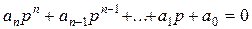(50)

Поэтому общее решение однородного уравнения (50) является линейной комбинацией экспоненциальных функций:

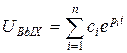(51)

Корни характеристического уравнения могут быть комплексными, вещественными или мнимыми. Условию устойчивости удовлетворяют только отрицательные вещественные корни или комплексные корни с отрицательной вещественной частью. Первые описывают апериодические изменения напряжения, вторые - затухающие колебания. Следовательно, эти корни соответствуют физическому критерию устойчивости, который гласит, что собственные колебания цепи должны быть затухающими. Таким образом, для устойчивой работы цепи необходимо, чтобы корни характеристического уравнения замкнутой цепи находились в левой полуплоскости комплексного переменного Р, что, в свою очередь, соответствует отрицательной вещественной части всех корней характеристического уравнения.

Теперь рассмотрим уравнение (48) с иной позиции. Колебаниям в цепях можно соотнести изображение по Лапласу. Запишем соответствие между оригиналом и изображением:

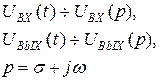
Вычислив преобразование Лапласа для обеих частей уравнения (48), получим

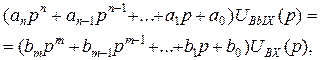
откуда находим коэффициент передачи в операторной форме

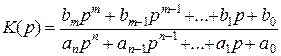(52)

Знаменатель этой дроби совпадает с характеристическим уравнением (50). Поэтому корни уравнения p_i можно рассматривать как полюса операторного коэффициента передачи. Тогда критерий устойчивости замкнутой цепи можно сформулировать следующим образом: все полюса коэффициента передачи замкнутой цепи должны находиться в левой полуплоскости плоскости комплексной частоты p.

2. Частотный критерий устойчивости (критерий Найквиста).

Алгебраический критерий устойчивости работы усилителя равносилен требованию, что модуль петлевого коэффициента усиления не должен обращаться в единицу в правой полуплоскости плоскости p. В этом случае в правой полуплоскости нет и полюсов функции K(p).

Для дальнейшего анализа учета ФЧХ петли ОС необходимо установить взаимно-однозначное соответствие плоскости комплексного переменного p=s+jw и плоскости 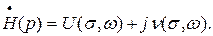Правая полуплоскость плоскости p ограничена мнимой осью (jw) и полуокружностью радиуса R®¥ [|R|= ].

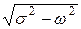При движении вдоль мнимой оси от jw до -jw функция 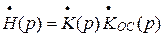плоскости Н отображается кривой, вид которой определяется функциональной зависимостью 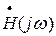. Следовательно мнимая ось плоскости p отображается на плоскости Н в кривую, заданную уравнением 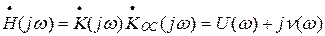или

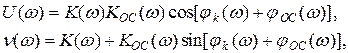
где j_k(w), j_OC(w) - фазочастотные характеристики усилителя и цепи ОС.

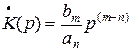На контуре бесконечно большого радиуса функции стремится к нулю. Действительно, R®¥ означает p®¥, а в этом случае в числителе и знаменателе формулы (52) имеет смысл сохранять только члены высшего порядка (так как pⁿ>>p^n-1>>...; p^m>>p^m-1>>...). Поэтому на окружности R®¥ функция примет вид . При n>m функция 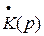, а следовательно и 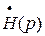стремятся к нулю при R®¥. Таким образом, полуокружность бесконечно большого радиуса на плоскости p отображается в точку начала координат на плоскости Н. Следовательно, поведение 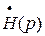однозначно определяется замкнутой кривой 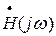на плоскости Н. В соответствии с правилом обхода контуров движение вдоль мнимой оси (сверху вниз) соответствует обходу замкнутой кривой при изменении частоты от +¥ до -¥. При этом вся правая полуплоскость плоскости p отображается во внутреннюю область замкнутой кривой .

Отсюда следует, что активная цепь устойчива, если ее петлевой коэффициент усиления не охватывает точку (1+j0). В противном случае цепь неустойчива.

Это условие называют критерием устойчивости Найквиста, а кривую называют диаграммой Найквиста (см. рис.).

Исходя из критерия Найквиста, обычно используют сравнительно простой способ определения частотной области устойчивости работы усилителя. Для устойчивости работы усилителя необходимо, чтобы в полосе рабочих частот выполнялось условие K(w)K_OC(w)<1 при j_k(w)+j_OC(w)=2p.

На рисунке приведены АЧХ и ФЧХ устойчивой и неустойчивой цепей

Л. 19-21

1. Генерирование колебаний в электрических цепях

4.1. Автоколебательная система - устройство с ОС.

В цепях, содержащих обратные связи, могут возникнуть изменяющиеся во времени электрические токи без воздействия на эти цепи внешних управляющих сигналов. Такие цепи называют автоколебательными системами, а колебания - автоколебаниями.

Типичная структура автоколебательной системы - это структура с обратной связью, в которой часть выходного сигнала возвращается на вход через цепь обратной связи (см. рис.).

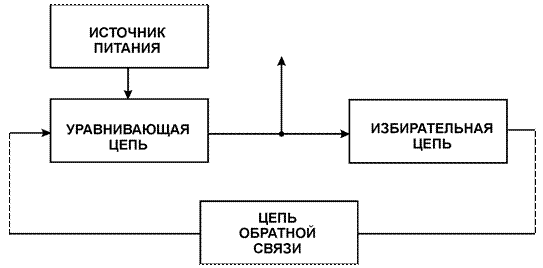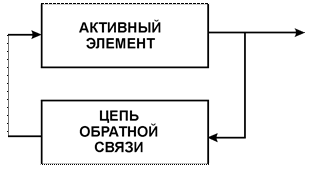В наиболее общем случае колебательная система включает источник питания, энергия которого, в конечном случае, и преобразуется в энергию колебаний, цепь управления этим преобразованием, избирательную цепь, служащую для отфильтровывания нужных колебаний, и цепь обратной связи. При анализе таких систем, как правило, источник питания рассматривают как составную часть управляющей цепи (активный управляющий элемент, например, усилитель), а избирательную цепь как составную часть либо активного элемента (колебательный контур в составе резонансного усилителя), либо цепи обратной связи (RC - автогенератором гармонических колебаний, мультивибратора и т.д.). Таким образом анализ колебательной системы сводится к анализу активной цепи с обратной связью (см. рис.).

С электротехнической точки зрения активный элемент колебательной системы является нелинейным четырехполюсником, коэффициент передачи которого зависит от действующих в его цепях токов и напряжений, а цепь обратной связи - линейным четырехполюсником. Эти свойства элементов системы определяют ее принцип действия.

Действительно, при соответствующем выборе параметров система с обратной связью становится неустойчивой. При этом малые амплитуды любых колебаний, существующих в системе, например, тепловых или коммутационных колебаний, начинают возрастать. С ростом амплитуды коэффициент передачи активного элемента, как правило, уменьшается, и при некотором его значении нарастание амплитуды колебаний прекращается. Установившиеся значение называется стационарным.

При анализе и расчете автоколебательных систем - автогенераторов решают две основные задачи:

1. определение условий при которых, устройство с обратной связью становится неустойчивым, т.е. самовозбуждаются;

2. определение амплитуды и частоты автоколебаний в стационарном режиме.

Наиболее сложной является вторая задача, в которой исследуется нелинейная система с обратной связью в режиме больших амплитуд, когда нелинейностью пренебречь нельзя. Первую же задачу решить относительно несложно, поскольку при малых амплитудах автоколебания на начальном этапе процесса нелинейный активный элемент может быть эквивалентно заменен линейной схемой замещения, такой как, например, у обычного линейного усилителя с ОС. Некоторые сведения об условиях самовозбуждения можно получить даже в общем случае, не рассматривая конкретной схемы автогенератора.

Действительно, коэффициент передачи по напряжению линейного четырехполюсника, охваченного обратной связью, определяется формулой:

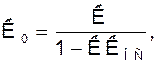
где 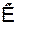- коэффициент передачи активного элемента автогенератора, а 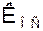- коэффициент передачи по цепи обратной связи.

В соответствии с алгебраическим критерием устойчивости система становится неустойчивой когда петлевой коэффициент передачи:

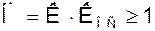(1)

В силу комплексности величины, входящих в (1), это соотношение разлагается на два условия:

- условие баланса амплитуд

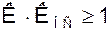(2)

- и условие баланса фаз

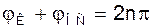(3).

Первое из них свидетельствует о том, что автоколебания в системе возможны, если активный элемент компенсирует все потери энергии в системе, включая нагрузку; второе условие требует, чтобы при этом колебания на входе и выходе петли обратной связи были синфазными.

В общем случае параметры 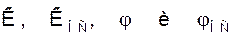зависят от частоты. Поэтому условия (2) и (3) обычно выполняются ил только для одной частоты или в достаточно узком диапазоне частот. Чтобы ответить на вопрос “на какой частоте возможны колебания?”, необходимо анализировать конкретную схему.

4.2. Самовозбуждение LC - автогенератора гармонических колебаний.

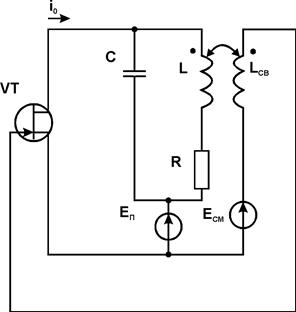Рассмотрим схему, в которой при определенных условиях могут возникать и существовать автоколебания. Схема содержащая полевой транзистор, колебательный контур и индуктивную цепь обратной связи. Будем считать, что ток стока транзистора связан с напряжением затвор-исток нелинейной зависимостью i₀=I(U_ЗИ).

В колебательном контуре уравнения, связывающие ток в емкости i_С c током i_L записывается в виде системы:

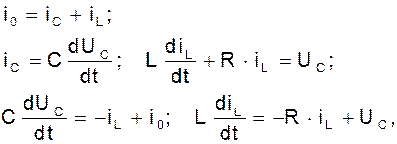
или как одно уравнение

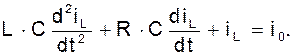
Для цепи обратной связи имеем

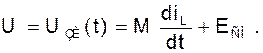
Следовательно, полную систему уравнений цепи можно записать таким образом:

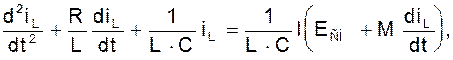(4)

или в развернутом виде:

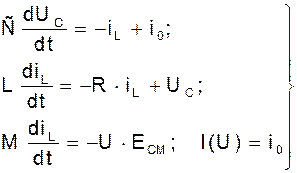(3)

После включения источников постоянного напряжения в цепи начинается заряд емкости и протекания тока в индуктивности, причем начальные значения i_L(t) и U_C(t) весьма малы. Напряжение U(t) при этом также будет незначительно отличаться от Е_СМ и зависимость I(U) может быть существенно упрощена.

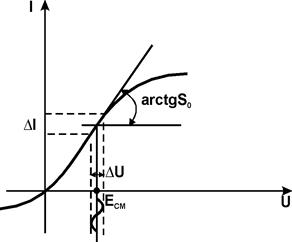
Пусть I(U)=a₀+a₁U+a₂U²+... (см. рис.). Так как

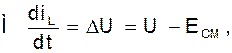
то

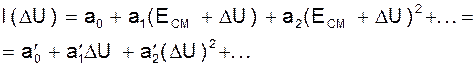
Если принять, что

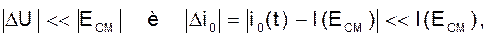
то можно линеаризовать зависимость i_C(t)-I(E_CM)=a^’₁DU=S₀DU, где S₀ - начальная крутизна, равная тангенсу угла наклона касательной к графику I(U) в точке U=E_СМ.

Дифференциальное уравнение для тока 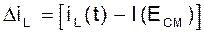будет таким:

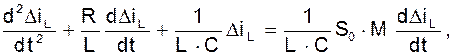
или

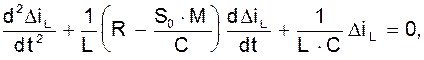(6).

Обозначим 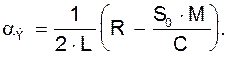Тогда уравнение (6) можно записать в виде:

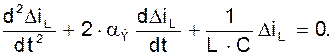
Это линеаризованное уравнение колебательного процесса в автогенераторе на стадии возникновения и нарастания колебаний. Его решения определяет закон суммирования амплитуды колебаний:

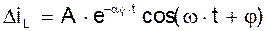
и их частоту

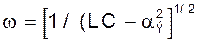
Начальные значения амплитуды и фазы колебаний можно найти из начальных условий. Но в рассматриваемом случае исходными следует считать случайными флуктуациями токов и напряжений, поэтому особого значения определения их величины не имеет.

Более важным является другое. Если a_Э>0, то какой бы ни была начальная флуктуация тока, процесс в цепи будет затухать. Если же a_Э<0, то сколь угодно малая начальная флуктуация тока будет нарастать с течением времени.

В первом случае цепь является устойчивой. Корни характеристического уравнения

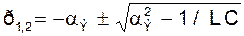
имеют отрицательную действительную часть.

Во втором случае цепь неустойчива. Неустойчивость может привести к автоколебаниям в цепи. Условием возникновения автоколебаний является положительность действительной части корней характеристического уравнения цепи. Рассмотрим физический смысл условия неустойчивости. Согласно уравнения (6), для возникновения автоколебаний необходимо иметь a_Э<0, т.е.

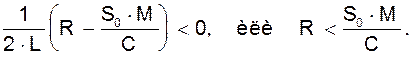
Сопротивление потерь в цепи, т.е. превращение энергии колебаний в теплоту, должно быть меньше некоторого значения, обусловленного крутизной характеристики активного элемента и коэффициентом обратной связи. Очевидно, что это условие эквивалентно условию баланса амплитуд вида (2). Фазовое условие существования автоколебаний вида (3) в данном анализе трансформировалось в выражение для частоты колебаний.

Полученное уравнение (6) справедливо только для малых приращений i_L(t). Поэтому решение в виде растущей экспоненты справедливо для цепи только на начальном этапе развития процесса автоколебаний. Амплитуда этих колебаний будет возрастать не бесконечно, а достигнет некоторого стационарного значения. Для расчета стационарной амплитуды и частоты колебаний в установившемся режиме используют другой метод, называемый гармонической линеаризацией.

4.3. Анализ стационарного режима автогенератора методом гармонической линеаризации

В методе гармонической линеаризации нелинейный резистивный четырехполюсник, включая и избирательный фильтр, заменяется некоторым эквивалентным линейным четырехполюсником с комплексной частотной характеристикой, зависящей от амплитуды входного сигнала. Рассмотрим, как осуществляется такая замена.

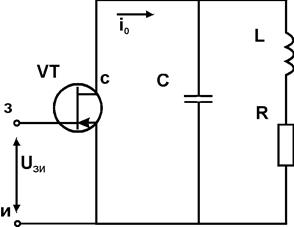Пусть имеется цепь, состоящая из полевого транзистора с колебательным контуром, включенным в цепь стока (см. рис.). Как и прежде нелинейная зависимость тока стока от напряжения затвор-исток задается многочленом i₀=I(U)= =a₀+a₁U+a₂U²+....

Можно показать (см. след. Раздел), что если напряжение затвор-исток гармоническое - U_ЗИ=U₀cos(w₀t+j₀), то ток истока будет определять гармоники с частотами w_i=iw₀:

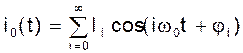
Если колебательный контур настроен на частоту первой гармоники 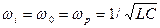, то на частоте w₀ сопротивление контура 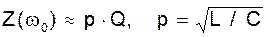. На частотах [(0, 2, 3... n) w₀], сопротивление контура будет близко нулю. При этом ток в индуктивности 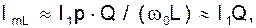где I₁ - амплитуда первой гармоники тока в нелинейном элементе. В свою очередь, амплитуда тока первой гармоники в нелинейном элементе зависит от вида характеристики этого элемента I(U), т.е. от коэффициентов а₁, а₃, а₅... и т.д., и от амплитуды входного сигнала U. Поэтому

I₁=I₁(а₁, а₃, а₅..., U).

Эта зависимость для заданного нелинейного элемента называется колебательной характеристикой. Для нелинейного четырехполюсника описываемого многочленом третьей степени, колебательная характеристика имеет следующий вид: (см. рис.).

Учитывая сказанное и принимая в качестве входного сигнала гармоническое колебание для тока стока бедам иметь:

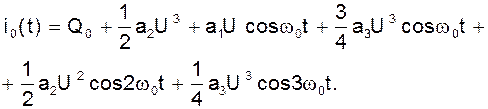
Относительно первой гармоники получаем

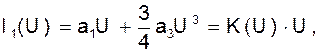
где 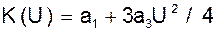- коэффициент передачи (крутизна ВАХ) нелинейного безынерционного элемента на первой гармонике (проводимость).

Таким образом, для каждой конкретной точки U^*=const колебательной характеристики (для которой К(U^*)=const), зависимость тока первой гармоники от входного напряжения имеет линейный характер I₁^*=K^*U^*.

Вернемся к схеме рассматриваемого автогенератора гармонических колебаний. Разомкнем цепь обратной связи и подключим по входу транзистора независимый источник гармонического напряжения e(t) (см. рис.).

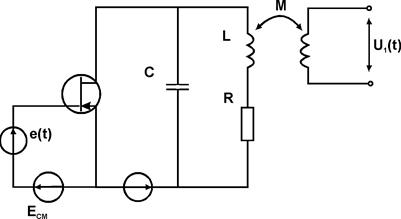Пусть e(t)=Ucosw₀t, . Тогда, согласно методу гармонической линеаризации ток в индуктивности где j₁ - сдвиг фазы между напряжением U₁ и током i_L. Напряжение 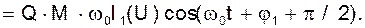Предположим, что амплитуда этого напряжения равна амплитуде входного напряжения, т.е. 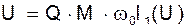, а 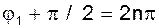. Тогда, если мгновенно отключить внешний источник e(t) и замкнуть обратной связи, то колебания в цепи будут продолжаться, как будто бы ничего не изменилось. Это условие стационарного режима: при обходе по петле обратной связи амплитуда остается неизменной, а сдвиг фаз кратен 2p.

Первое условие, как и ранее, является условием баланса амплитуд, второе - условием баланса фаз:

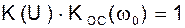(7)

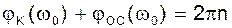(8)

Здесь K(U) - коэффициент передачи (крутизна ВАХ) безынерционного нелинейного элемента по первой гармонике; K_OC(w₀) - коэффициент передачи цепи обратной связи; j_к - фазовый сдвиг нелинейного элемента, а j_ОС(w₀) - фазовый сдвиг в цепи обратной связи.

Из уравнений (7) и (8) определяется стационарная амплитуда U и стационарная частота w₀ колебаний. Для рассматриваемой цепи имеем:

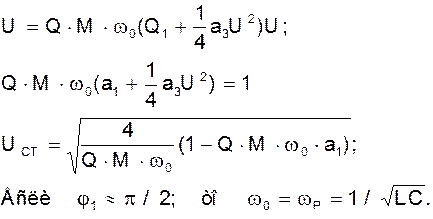
4.4 Графический метод анализа стационарного режима.

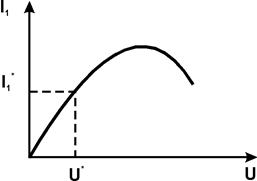
Понятие колебательной характеристики линейной цепи позволяет определить стационарную амплитуду в цепи с обратной связью графическим методом.

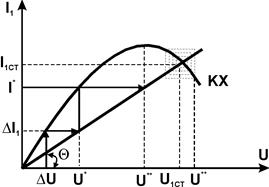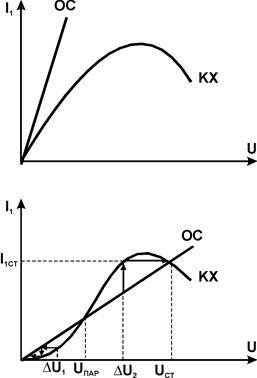
По определению, колебательная характеристика есть зависимость амплитуды первой гармоники выходного тока I₁ нелинейного элемента от амплитуды U входного гармонического напряжения. Поэтому для графического решения уравнения баланса амплитуд необходима характеристика обратной связи, представляющая собой зависимость амплитуды напряжения обратной связи U от амплитуды тока I₁. Поскольку цепь обратной связи линейная, искомая зависимость представляет собой прямую линию, проходящую через начало координат. Угол наклона ее зависит от способа реализации обратной связи. В нашем случае 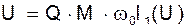и 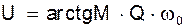и прямой обратной связи (см. рис.). Графики будут иметь две точки пересечения: начало координат и некоторую точку U_CT, I_CT. Эти точки соответствуют двум возможным стационарном состояниям цепи: первая - отсутствию колебаний, вторая - стационарным автоколебаниям с амплитудой U_CT. Покажем, что первая точка является неустойчивой. Пусть имеется небольшая начальная флуктуация DU. Ей будет соответствовать появление тока с амплитудой первой гармоники DI₁. Этот ток создает в цепи обратной связи напряжение U^*, которое приведет к появлению тока I^* и т.д. Таким образом, малая начальная флуктуация DU приведет к установлению стационарной ненулевой амплитуды колебаний.

Для того, чтобы нулевая точка была неустойчивой, прямая обратной связи должна проходить в начале координат ниже графика колебательной характеристики:

Это условие самовозбуждения было уже получено из анализа корней характеристического многочлена дифференциального уравнения цепи.

Рассмотренная цепь считается находящейся в мягком режиме самовозбуждения, когда колебания возникает при . Очевидно (из построений), что точка U_СТ, I_СТ является устойчивой, поскольку любые DU приводят к ее возврату в прежнее положение.

Расположение линии обратной связи по отношении к колебательной характеристике может быть и иным (см. рис.). В этом случае стационарный режим будет при нулевой амплитуде. В цепи, не возникает автоколебаний при любых отклонениях DU.

Если график колебательной характеристики I₁(U) имеет S - образную форму (см. след. Рис.), но начальная точка будет устойчивой, однако цепь может самовозбудиться, если в ней возникнет начальная флуктуация DU>U_пар. Режим, когда начальная точка является устойчивой, но существует пороговое значение флуктуаций, превышение которого приводит к самовозбуждению, называется жестким режимом возбуждения генератора.

Таким образом, нелинейная цепь может вести себя по разному при малых и сильных внешних воздействий. Если по линеаризованному дифференциальному уравнению можно установить устойчивость или неустойчивость цепи “в малом”, то анализ колебательной характеристики совместно с прямой обратной связи позволяет провести анализ устойчивости “ в большом” и определить возможность существования жесткого режима возбуждения.

Метод гармонической линеаризации пригоден для анализа цепей с узкополосными фильтрами - колебательными контурами с высокой добротностью. Если же фильтр не является таким контуром, то автоколебания будут возникать не только на первой гармонике, но и на других (w=nw₀). При этом....... колебаний будет негармонической. Для анализа процессов в таких цепях используют метод уравнений состояния и их численное интегрирование.

4.5. Анализ автоколебаний методом уравнений состояния

Уравнение (4), получение для автоколебательной цепи, эквивалентно системе уравнений первого порядка:

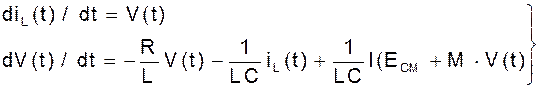(9)

Такое представление уравнений цепи соответствует уравнениям состояния.

В силу нелинейного характера функции I(U) найти решение (9) аналитически нельзя. Для анализа процессов применяют численные методы интегрирования систем дифференциальных уравнений - численное моделирование.

Простейший подход состоит в приближенной замене производной от функции f(t):

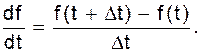
Обозначим получим

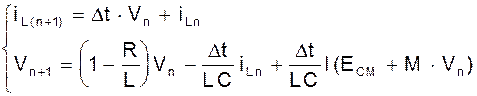(10)

Предположим, что известна начальная флуктуация i_L(0)=i₀; V(0)=0. Поскольку функция I(U) может быть вычислена для любых значений аргумента, подставляя в (10), получаем:

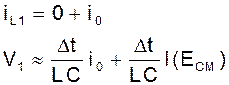
Теперь, подставив полученные значения снова в (10), найдем i_L2, V₂ и т.д. Этот метод приближенного решения носит название метода Эйлера.

Решение системы уравнений вида (10) может быть представлено графически на плоскости состояния (см. рис.).

Рассмотрение процессов в автоколебательных цепях на плоскости состояния часто оказывается более наглядным, чем в другой форме.

Рассмотрим примеры, показывающие взаимосвязь характеристики и линии ОС с траекторией на плоскости состояния и осциллограммы процессов, полученных численным решением уравнений состояния.

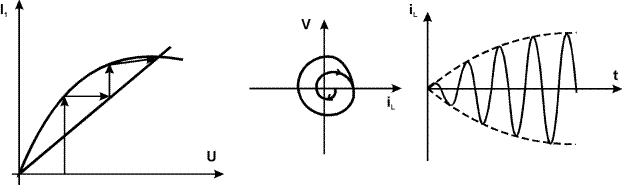1. Автоколебательная цепь в мягком режиме самовозбуждения с монотонным установлением амплитуды.

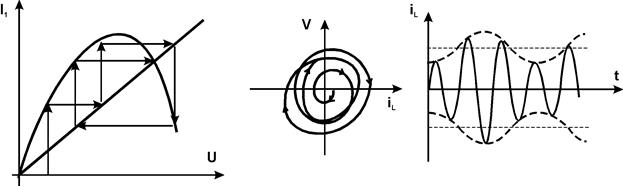2. Мягкий режим самовозбуждения с немонотонным установлением амплитуды

3. Жесткий режим с монотонным установлением колебаний

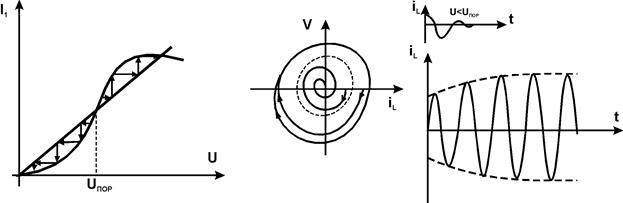4.6. RC - автогенераторы гармонических колебаний

Гармонические колебания можно получить в системах, не содержащих колебательного контура. Выделение колебания нужной частоты здесь основано на том, что условия самовозбуждения (2) и (3) в ряде случаев могут выполнять только на одной частоте.

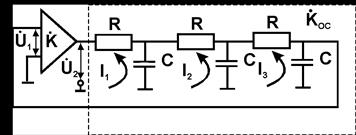Рассмотрим вариант такой системы (см. рис.) состоящий из усилителя с коэффициентом передачи 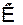и цепи обратной связи с коэффициентом передачи 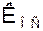. Чтобы воспользоваться формами (2) и (3) примем, что 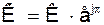и определим 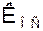. Для этого воспользуемся методом контурных токов, в соответствии с которым составим систему уравнений, связывающих

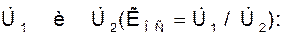
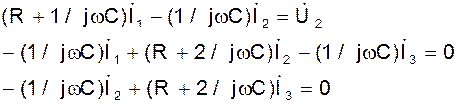
решая эту систему относительно 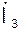, находим

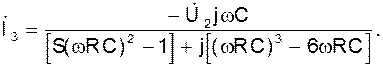
Так как 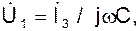то

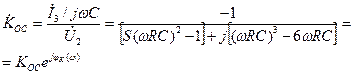(11)

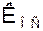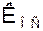Так как фазовый сдвиг, вносимый усилителем, составляет p рад, то условие самовозбуждения (3) будет выполнено, если j_OC(w)= =arctg(Im /Re )=p.

Как следует из (11) последнее выполняется при условии

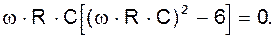
Откуда для частоты генерации находим:

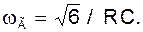(12)

Подставляя (12) в (11) находим значения модуля передаточной функции:

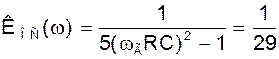(13)

Используя (13) в (2) находим коэффициент усиления усилителя, при котором возможна генерация:

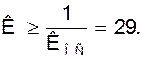
Аналогичным образом анализируется и другие схемы RC - автогенераторов.

Л. 22-24

5. Анализ нелинейных цепей

5.1. Общие понятия об элементах нелинейных цепей

Цепи, которые изучались ранее, относятся к классу линейных цепей. Параметры элементов этих цепей. Параметры элементов этих цепей - сопротивлений, индуктивностей, емкостей - не зависит от значений приложенных к ним напряжений или протекающих через них токов.

В действительности любой реальный элемент таким постоянством не обладает и линейная теория оказывается справедливой только в определенных пределах значений напряжений и токов. Существует также обширный класс исключительно важных элементов и устройств, параметры, которых существенно зависят от токов или напряжений. Такие элементы называются нелинейными. Им нельзя приписать какой-то постоянный параметр даже при изменении переменных в ограниченном диапазоне. Для количественного описания свойств нелинейных элементов необходимо задавать зависимости, называемые характеристиками. Рассмотрим в общем виде характеристики основных нелинейных идеализированных элементов.

5.2. Модели нелинейных элементов

5.2.1 Нелинейный резистивный элемент (НЭ) полностью определяется зависимостью между током i и напряжением U (т.е. ВАХ): i=i(U) или U=U(i). Резистивный НЭ обозначается: . Одна из форм ВАХ может быть, например, такой (см. рис.).

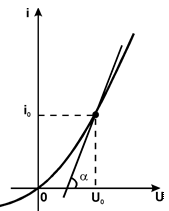
Определить нелинейный резистивный элемент - значит задать его вольтамперную характеристику полностью. В каждой точке ВАХ, заданной конкретным значением напряжения и тока U=U₀, i=i(U₀)=i₀, можно ввести понятие статического сопротивления

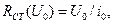
и динамического (дифференциального) сопротивления, равного котангенсу угла наклона касательной к ВАХ в данной точке: (см. рис.)

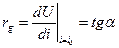
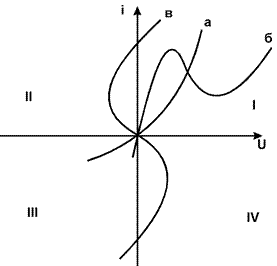Общая классификация видов ВАХ резистивных НЭ рассматривает их свойства по положению ВАХ по квадрантам в плоскости (U, i), (см. рис.). Если график располагается только в первом и третьем квадрантах, то ВАХ относится к пассивному элементу, поскольку потребляемая мощность 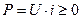(а,б). Для пассивного элемента i(0)=0. Если же часть графика попадает во второй, или в четвертый квадрант, то говорят, что элемент является активным (в). Это означает, что в его цепи есть источник ‘ электрической энергии.

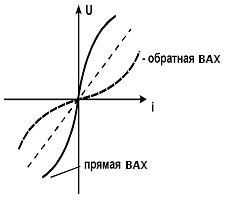
Другим общим свойством резистивных НЭ является монотонность или немонотонность ВАХ.

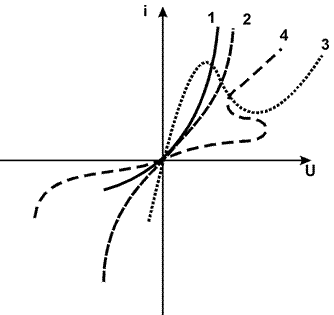Немонотонные ВАХ имеют знакопеременное дифференциальное сопротивление. На предыдущем рисунке показаны три типа ВАХ по монотонности: а - монотонная, б - N - образная, в - S - образная.

Монотонность ВАХ играет особую роль при анализе цепей, поскольку при решении уравнений приходится оперировать зависимостями U=U(i) и наоборот i=i(U). Зависимость, обратная к монотонной, также монотонная и особых проблем при обращении не возникает. Для немонотонных зависимостей необходимо решать уравнения с многозначными функциями. Геометрически, обращение монотонной ВАХ соответствует симметричному отражению графика около биссектрисы первого - третьего квадрантов (см. рис.).

Реально в качестве резистивных НЭ используются диоды (1), варисторы (2), туннельные диоды (3), денисторы (4) (см. след. рис.).