Преобразования Галилея. Механический принцип относительности

- классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы дианамики одинаковы во всех инерциальных систе­мах отсчета.

Для его доказательства рассмотрим две системы отсчета: инерциальную систему К (с координатами 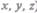), которую условно будем считать неподвижной, и систему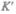

(с координатами 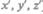), движущуюся относительно К равномерно и прямолинейно со

скоростью 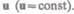Отсчет времени начнем с момента, когда начала координат

обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость ■ направлена вдоль 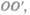радиус-вектор, проведенный из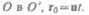

Найдем связь между координатами произвольной точки А в обеих системах. Из I рис. 58 видно, что

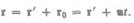(34.1)

Уравнение (34.1) можно записать в проекциях на оси координат:

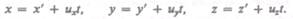(34.2) |