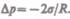Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна

(682)

Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину

Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа*, опре­деляющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

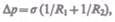(68.3) где — радиусы кривизны двух любых взаимно перпендикулярных нормальных

*П. Лаплас (1749—1827) — французский ученый.

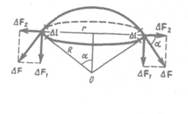
Сечений поверхности жидкости в данной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.

Для сферической искривленной поверхности 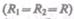выражение (68.3) перехо-

дит в (68.1), для цилиндрической 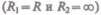- избыточное давление

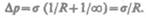
В случае плоской поверхности 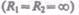силы поверхностного натяжения избыточ-