Интегрирование алгебраических и трансцендентных иррациональных функций в некоторых известных случаях сводится к интегрированию рациональных дробей.
I. Интеграл вида 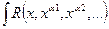 dx, где R – рациональная функция,
dx, где R – рациональная функция, 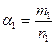 ,
, 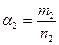 ,… — рациональные числа, сводится к интегралу от рациональной функции с помощью подстановки
,… — рациональные числа, сводится к интегралу от рациональной функции с помощью подстановки 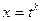 , где k -общий знаменатель дробей
, где k -общий знаменатель дробей 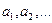

Пример
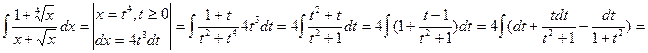 =
= 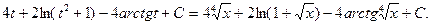
Найти интегралы.
82. 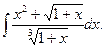 83.
83. 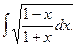
К интегралам от функций, рационально зависящим от тригонометрических функций, сводятся интегралы:
III. 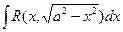 — подстановкой
— подстановкой 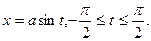
IV*. 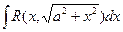 — подстановкой
— подстановкой 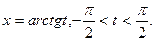
V*. 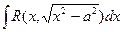 — подстановкой
— подстановкой 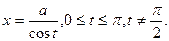
Примеры.
1.
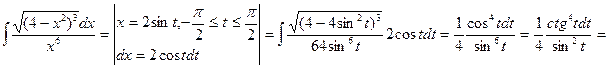
= 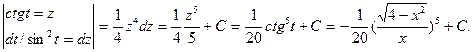
При решении выполнили преобразования: при 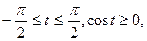
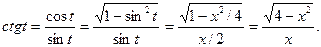
2.
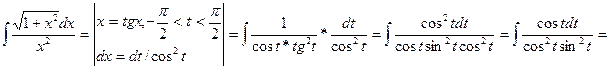
= 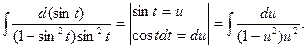
В решении использовано: 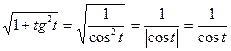 при
при 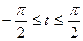 .
.
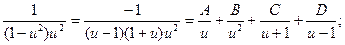
-1= 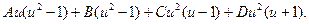
Пусть u = 0; тогда -1 = - B, B = 1.
u = -1; тогда - 1 = 2D, D = -1/2.
u = -1; тогда -1 = -2С, С = 1/2.
Приравняем коэффициенты при 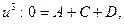 отсюда А = 0.
отсюда А = 0.
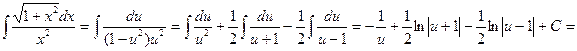
= — 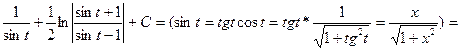
= - 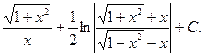
Найти интегралы:
84. 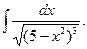 85*.
85*. 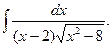
VI. Интегралы вида 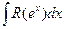 можно вычислить подстановкой
можно вычислить подстановкой 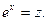 При этом
При этом 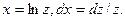
Пример.
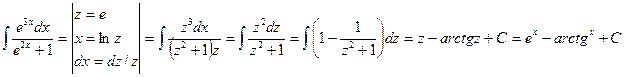
Найти интегралы:
86. 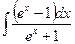 . 87.
. 87. 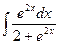 .
.
Замечание. Не всякая элементарная функция имеет интеграл, выраженный через элементарные функции.
Примеры
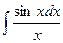 ,
, 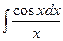 ,
, 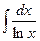 ,
, 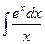 ,
, 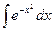 ,
, 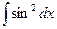 ,
, 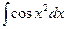 ,
, 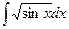 ,
, 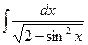 ,
, 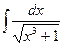 .
.
Вышеприведенные интегралы не выражаются суммой конечного числа элементарных функций и называются «не берущимися» интегралами.
Вопросы и задания для самоконтроля
1. Какие замены переменных можно сделать для нахождения следующих интегралов:
а) 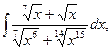 б)*
б)* 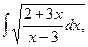 в)*
в)* 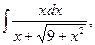 г)
г) 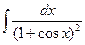 ?
?
2. Можно ли вычислить в элементарных функциях следующие интегралы:
а) 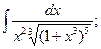 б)
б) 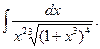
 2015-02-04
2015-02-04 937
937








