Сложение гармонических колебаний с равными частотами

Пусть складываются два скалярных гармонических колебания с одной и той же частотой w₀:

.

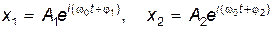(21.18)

В соответствии с принципом суперпозиции результирующее колебание

.

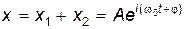(21.19)

Здесь A и j — амплитуда и начальная фаза результирующего колебания, которые подлежат определению. Для решения этой задачи подставим (21.18) в (21.19). После сокращения на 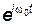получим

.

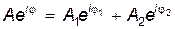(21.20)

Приравняем в (21.20) действительные и мнимые части, используя формулу Эйлера (см. математическое введение):

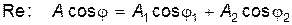;	(21.21)
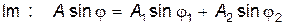.	(21.22)

Начальную фазу найдем, разделив (21.22) на (21.21):

.

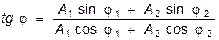(21.23)

Результирующую амплитуду A найдем, если возведем (21.21) и (21.22) в квадрат и сложим. После несложных преобразований получим

.

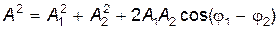(21.24)

Рассмотрим теперь частные случаи.

а) Начальные фазы совпадают j₁=j₂ (или отличаются на 2kp).

Тогда из (21.24) следует

,

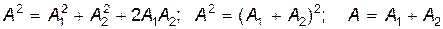т.е. результирующая амплитуда равна сумме амплитуд складываемых колебаний — происходит взаимное усиление колебаний (рис. 21.8, а).

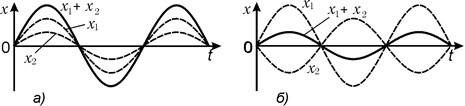
Рис. 21.8

б) Начальные фазы противоположны j₁-j₂ =p, 3p,..., (2k+1)p.

Тогда из (21.24) следует

,

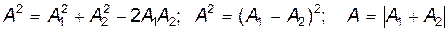т.е. результирующая амплитуда равна разности амплитуд складываемых колебаний — происходит взаимное ослабление колебаний (рис. 21.8, б).