Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной, например, функция 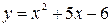 .
.
Функция 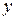 аргумента
аргумента 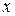 называется неявной, если она задана уравнением
называется неявной, если она задана уравнением 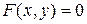 , не разрешенным относительно зависимой переменной. Например,
, не разрешенным относительно зависимой переменной. Например, 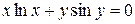 .
.
Обратная функция. Пусть между переменными 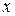 и
и 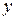 , заданными уравнением
, заданными уравнением 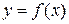 , существует взаимно-однозначное соответствие. Рассмотрим для примера функцию
, существует взаимно-однозначное соответствие. Рассмотрим для примера функцию 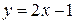 , выразим в этом уравнении переменную
, выразим в этом уравнении переменную 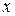 через
через 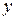 :
: 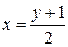 . Это уравнение, как и
. Это уравнение, как и 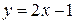 , описывает одну совокупность точек на координатной плоскости. Связь между переменными одна и та же, различия лишь в форме записи. Эту функцию
, описывает одну совокупность точек на координатной плоскости. Связь между переменными одна и та же, различия лишь в форме записи. Эту функцию 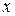 от аргумента
от аргумента 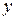 называют обратной по отношению к исходной. В уравнении
называют обратной по отношению к исходной. В уравнении 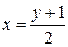 задаем значение переменной
задаем значение переменной 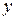 , вычисляем значение переменной
, вычисляем значение переменной 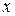 . Обозначим независимую переменную через
. Обозначим независимую переменную через 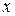 , зависимую через
, зависимую через 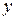 и перепишем уравнение в виде
и перепишем уравнение в виде 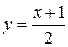 . Под обратной функцией будем подразумевать именно такую функцию. В общем виде, имея
. Под обратной функцией будем подразумевать именно такую функцию. В общем виде, имея 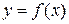 , можем выразить
, можем выразить 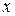 через
через 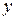 , введя специальное обозначение
, введя специальное обозначение 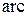 , т.е.
, т.е. 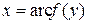 . Это другая форма записи исходной функциональной зависимости. Поменяем переменные:
. Это другая форма записи исходной функциональной зависимости. Поменяем переменные: 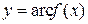 . Перед нами обратная функция, ее обозначают также в виде
. Перед нами обратная функция, ее обозначают также в виде 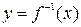 . Для любой строго монотонной функции существует обратная функция. Графики взаимно-обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
. Для любой строго монотонной функции существует обратная функция. Графики взаимно-обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Сложная функция. Пусть функция 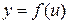 есть функция от переменной
есть функция от переменной 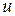 , определенной на множестве
, определенной на множестве 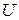 с областью значений
с областью значений 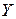 , а переменная
, а переменная 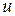 является функцией
является функцией 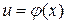 от переменной
от переменной 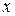 , определенной на множестве
, определенной на множестве 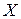 с областью значений
с областью значений 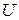 . Тогда заданная на множестве
. Тогда заданная на множестве 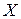 функция
функция 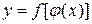 называется сложной функцией аргумента
называется сложной функцией аргумента 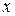 . Например,
. Например, 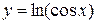 - сложная функция.
- сложная функция.
Основные свойства функций:
1) Четность и нечетность. Функция 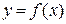 называется четной, если для любых значений
называется четной, если для любых значений 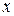 из области определения
из области определения 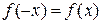 и нечетной, если
и нечетной, если 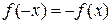 . В противном случае функция
. В противном случае функция 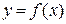 называется функцией общего вида.
называется функцией общего вида.
Пример. а) Функция 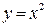 - четная (рис. 2.2 а)), т.к
- четная (рис. 2.2 а)), т.к 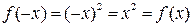 ;
;
б) Функция 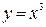 - нечетная (рис. 2.2 б)), т.к.
- нечетная (рис. 2.2 б)), т.к. 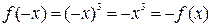 ;
;
в) Функция 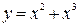 - общего вида (рис. 2.2 в)), т.к.
- общего вида (рис. 2.2 в)), т.к. 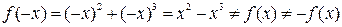 .
.
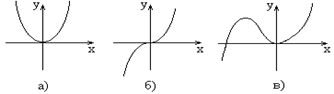
Рис. 2.2
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
2) Монотонность. Функция 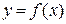 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке 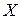 , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
Пример. 1) Функция 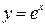 - на интервале
- на интервале 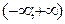 монотонно возрастает (рис. 2.3 а)).
монотонно возрастает (рис. 2.3 а)).
2) Функция 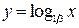 - на интервале
- на интервале 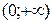 монотонно убывает (рис. 2.3 б)).
монотонно убывает (рис. 2.3 б)).
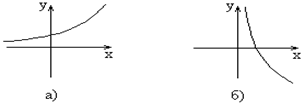
Рис. 2.3
3) Ограниченность. Функция 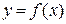 называется ограниченной на промежутке
называется ограниченной на промежутке 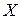 , если существует такое положительное число
, если существует такое положительное число 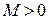 , что
, что 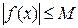 для любого
для любого 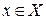 . В противном случает функция называется неограниченной. Например,
. В противном случает функция называется неограниченной. Например, 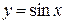 - ограничена на всей числовой оси, т.к.
- ограничена на всей числовой оси, т.к. 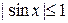 для любого
для любого 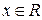 .
.
4) Периодичность. Функция 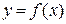 называется периодической с периодом
называется периодической с периодом 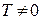 , если для любых
, если для любых 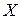 из области определения функции
из области определения функции 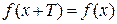 .
.
Пример. Функция 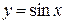 , период
, период 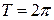 , т.к. для любых
, т.к. для любых 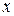
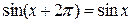 (рис. 2.4).
(рис. 2.4).
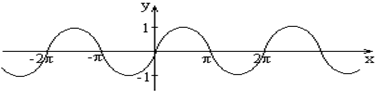
Рис. 2.4
 2015-02-14
2015-02-14 1787
1787
