Из основных функции новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операции образования сложной функции.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Пример.
1) 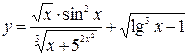 - элементарная функция, т.к. число операций сложения, вычитания, умножения, деления и образования сложной функции
- элементарная функция, т.к. число операций сложения, вычитания, умножения, деления и образования сложной функции 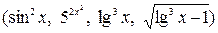 конечно.
конечно.
2) 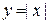 - неэлементарная функция.
- неэлементарная функция.
Основные элементарные функции:
1) Постоянная функция: 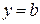 .
.
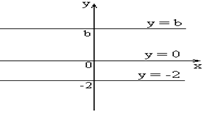 | Графиком постоянной функции 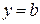 является прямая, параллельная оси абсцисс и проходящая через точку является прямая, параллельная оси абсцисс и проходящая через точку 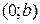 на оси ординат. на оси ординат. |
2) Степенная функция.
а) Степенная функция с натуральным показателем 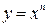 (
(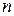 – натуральное число:
– натуральное число: 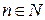 ). (непериодическая)
). (непериодическая)
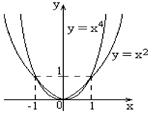 | 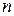 – четное число Область определения – четное число Область определения 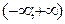 . Область значений . Область значений 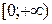 . Монотонность: убывает на . Монотонность: убывает на 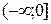 , возрастает на , возрастает на 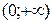 . Четная. . Четная. |
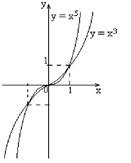 | 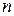 – нечетное число Область определения – нечетное число Область определения 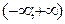 . Область значений . Область значений 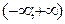 . Монотонность: возрастает на . Монотонность: возрастает на 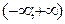 . Нечетная. . Нечетная. |
б) Степенная функция с целым отрицательным показателем 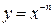 (
(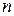 – натуральное число:
– натуральное число: 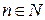 ). (непериодическая)
). (непериодическая)
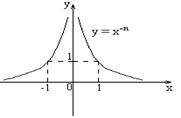 | 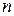 – четное число Область определения – четное число Область определения 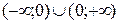 . Область значений . Область значений 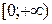 . Монотонность: возрастает на . Монотонность: возрастает на 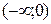 , убывает на , убывает на 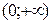 . Четная. . Четная. |
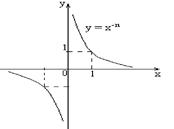 | 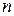 – нечетное число Область определения – нечетное число Область определения 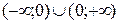 . Область значений . Область значений 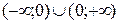 . Монотонность: убывает на . Монотонность: убывает на 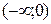 и на и на 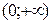 . Нечетная. . Нечетная. |
в) Степенная функция с положительным показателем меньше единицы 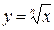 (
(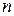 – натуральное число больше единицы:
– натуральное число больше единицы: 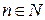 ,
, 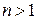 ). (непериодическая).
). (непериодическая).
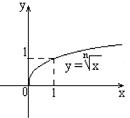 | 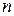 – четное число Область определения – четное число Область определения 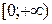 . Область значений . Область значений 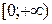 . Монотонность: возрастает на . Монотонность: возрастает на 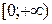 . Общего вида. . Общего вида. |
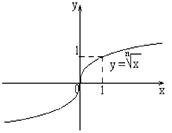 | 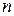 – нечетное число Область определения – нечетное число Область определения 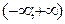 . Область значений . Область значений 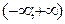 . Монотонность: возрастает на . Монотонность: возрастает на 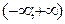 . Нечетная. . Нечетная. |
3) Показательная функция 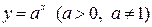 . (непериодическая).
. (непериодическая).
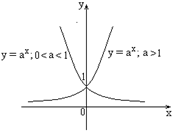 | Область определения 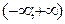 . Область значений . Область значений 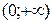 . Монотонность: возрастает на . Монотонность: возрастает на 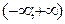 , если , если 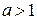 ; убывает на ; убывает на 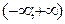 , если , если 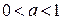 . Общего вида. . Общего вида. |
4) Логарифмическая функция 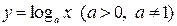 . (непериодическая).
. (непериодическая).
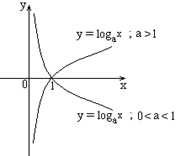 | Область определения 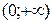 . Область значений . Область значений 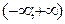 . Монотонность: возрастает на . Монотонность: возрастает на 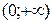 , если , если 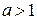 ; убывает на ; убывает на 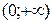 , если , если 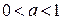 . Общего вида. . Общего вида. |
5) Тригонометрические функции. (периодические).
а) синус 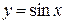 . Период равен . Период равен 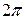 . . | ||
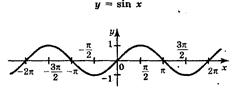 | Область определения 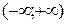 . Область значений . Область значений 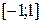 . Монотонность: возрастает на . Монотонность: возрастает на 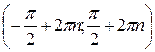 ; убывает на ; убывает на 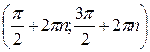 . Нечетная. . Нечетная. | |
б) косинус 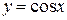 . Период равен . Период равен 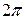 . . | ||
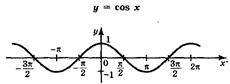 | Область определения 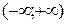 . Область значений . Область значений 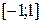 . Монотонность: возрастает на . Монотонность: возрастает на 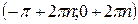 ; убывает на ; убывает на 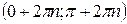 . Четная. . Четная. | |
в) тангенс 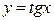 . Период равен . Период равен 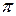 . . | ||
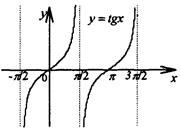 | Область определения 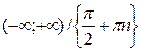 . Область значений . Область значений 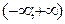 . Монотонность: возрастает на . Монотонность: возрастает на 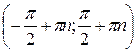 . Нечетная. . Нечетная. | |
г) котангенс 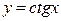 . Период равен . Период равен 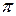 . . | ||
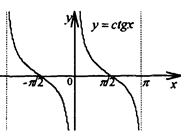 | Область определения 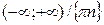 . Область значений . Область значений 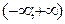 . Монотонность: убывает на . Монотонность: убывает на 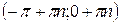 . Нечетная. . Нечетная. | |
6) Обратные тригонометрические функции. (непериодические).
а) арксинус 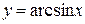 . . | |
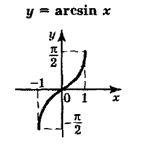 | Область определения 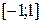 . Область значений . Область значений 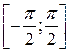 . Монотонность: возрастает на . Монотонность: возрастает на 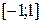 . Нечетная. . Нечетная. |
б) арккосинусом 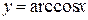 . . | |
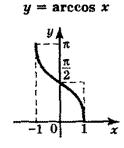 | Область определения 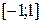 . Область значений . Область значений 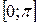 . Монотонность: убывает на . Монотонность: убывает на 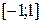 . Общего вида. . Общего вида. |
в) арктангенс 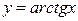 . . | |
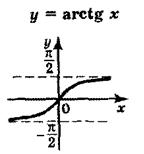 | Область определения 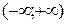 . Область значений . Область значений 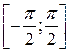 . Монотонность: возрастает на . Монотонность: возрастает на 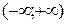 . Нечетная. . Нечетная. |
г) арккотангенс 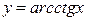 . . | |
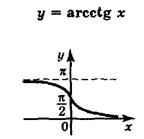 | Область определения 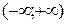 . Область значений . Область значений 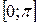 . Монотонность: убывает на . Монотонность: убывает на 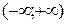 . Общего вида. . Общего вида. |
 2015-02-14
2015-02-14 9366
9366
