Представление исходной задачи в виде симплекс таблицы

Для получения исходной симплекс-таблицы общую или стандартную задачу линейного программирования необходимо привести к каноническому виду путем введения дополнительных неотрицательных переменных.

Если задача линейного программирования изначально задана в канонической форме, то необходимо выделить базисные переменные в системе ограничений, используя, к примеру, метод Жордана-Гаусса.

Пусть с помощью метода Жордана-Гаусса в системе ограничений задачи (5.15) выделили базисные переменные х₁, х₂, …, х_m:

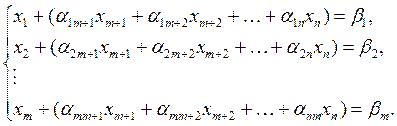(5.16)

где 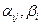– полученные в результате элементарных преобразований значения величин a_ij и b_i соответственно (причем 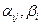- не обязательно положительные);

x_m+1, x_m+2, …, x_n – свободные переменные.

Выразим в системе (5.16) базисные переменные через свободные:

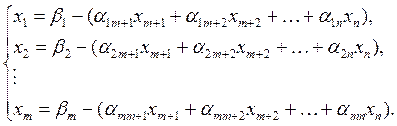(5.17)

Подставим в целевую функцию задачи линейного программирования (5.15) полученные значения базисных переменных, приведем подобные, в результате получим:

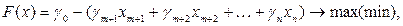(5.18)

где 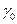- сумма величин ;

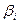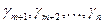– полученные в результате преобразований значения коэффициентов при переменных x_m+1, x_m+2, …, x_n соответственно;

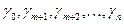– не обязательно положительные.

Представим полученные систему ограничений и целевую функцию в виде следующей таблицы:

Таблица 5.1

Исходная симплекс-таблица

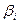
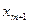
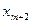
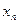
Свободные переменные Базисные переменные	Свободные числа,					Оценочные отношения,

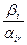
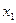
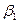
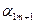
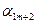
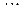
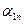
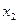
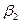
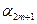
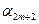
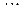
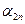
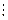
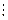
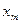
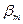
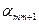
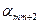
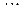
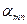
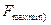
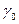
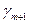
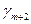
Примечание: величины 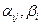и 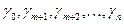в таблице приводятся со своими знаками, которые они имеют в системе ограничений (5.17) и целевой функции (5.18) без раскрытия скобок.

Данную таблицу называют симплекс-таблицей, на основе которой проводятся последующие преобразования.