Этап: составление исходной симплекс-таблицы

Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х₁ и х₂.

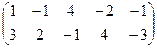
Умножим (поэлементно) первую строку на –3 и сложим со второй:

.

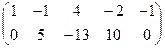Умножим вторую строку на :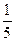

.

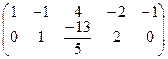Сложим вторую с первой строкой:

.

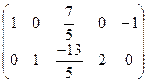В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

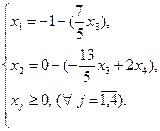
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

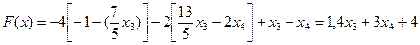Запишем целевую функцию в следующем виде:

.

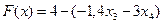Составим исходную симплекс-таблицу:

Таблица 5.11

Исходная симплекс-таблица

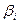
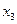
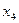
СП БП				Оценочные отношения
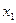
	–1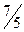
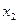
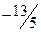
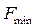
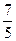
		–	–3