Реверсивный счетчик сочетает в себе свойства суммирующего и вычитающего счетчиков. Реверсивные счетчики строятся двумя способами. В первом случае счетчик имеет один счетный и один управляющий вход, причем, в зависимости от сигнала на управляющем входе, счетчик работает либо в режиме суммирования, либо в режиме вычитания. Во втором случае счетчик имеет два счетных входа; при подаче счетных импульсов на один из входов они суммируются, при подаче на другой-вычитаются.
Рассмотрим синтез счетчика первого варианта, работающего в коде ''4-2-1'', с Ксч=8, на JK триггерах.
Условимся, что при подаче на управляющий вход Р счетчика сигнала ''1'' счетчик работает в режиме суммирования, а при Рn =0 – в режиме вычитания. Заметим, что случаю Рn =1, соответствует таблица функционирования суммирующего счетчика (см. табл. 3), а при Рn =0-вычитающего счетчика (табл.4). Следовательно, при сигнале управления Рn =1, необходимо обеспечить уравнение входов суммирующего счетчика (2.7), а Рn =0-уравнения входов вычитающего счетчика (2.8).
Уравнения входов реверсивного счетчика, при известных уравнениях входов однотипных суммирующих и вычитающих счетчиков, находятся следующим образом:
Для п е р в о г о р а з р я д а, сравнивая (2.5) и (2.7) замечаем, что как при Рn =1, так и при Рn =0, 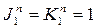 ,следовательно уравнения входов не зависят от сигнала управления и можно записать:
,следовательно уравнения входов не зависят от сигнала управления и можно записать:
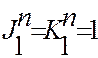 (2.9)
(2.9)
Для в т о р о г о р а з р я д а:
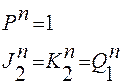
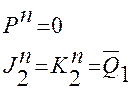 (2.10)
(2.10)
Таким образом, можно сказать, что Jn и Kn зависят от двух переменных- P, Q1, т.е. 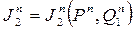 ;
; 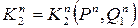 - двоичные функции двух аргументов, и для их аналитического выражения надо составить таблицу, где каждому (из 4-х возможных) двоичному набору переменных
- двоичные функции двух аргументов, и для их аналитического выражения надо составить таблицу, где каждому (из 4-х возможных) двоичному набору переменных 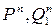 , ставилось, в соответствии с (2.10) значение
, ставилось, в соответствии с (2.10) значение 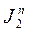 и
и 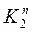 . Перенося затем эти значения в диаграммы Вейча (см. п. 2.5.) и минимизируя получим уравнения входов для
. Перенося затем эти значения в диаграммы Вейча (см. п. 2.5.) и минимизируя получим уравнения входов для 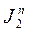 и
и 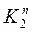 в виде ДНФ.
в виде ДНФ.
Результаты представлены в таблице 5 и рис.13.
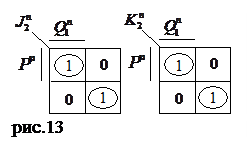
 Уравнения входов второго разряда имеют вид:
Уравнения входов второго разряда имеют вид:
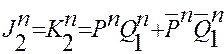
(2.11)
Для третьего разряда, совершенно аналогично, но 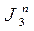 и
и 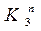 являются функциями трех переменных
являются функциями трех переменных 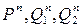 , т.е.
, т.е.
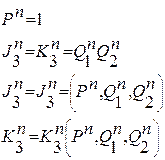
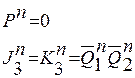 (2.12)
(2.12)
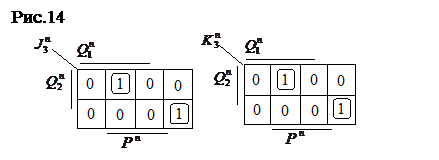 |
Для нахождения их аналитического выражения, составим таблицу, в которой каждому (из 8 возможных) наборов переменных
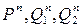 ставится(по 2.12) в соответствие значения
ставится(по 2.12) в соответствие значения 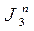 и
и 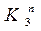 .Результаты приведены в таблице6 и рис.14.
.Результаты приведены в таблице6 и рис.14.
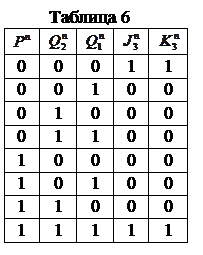 Следовательно, уравнения входов третьего разряда имеют вид:
Следовательно, уравнения входов третьего разряда имеют вид:
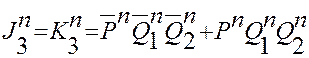 (2.13)
(2.13)
По уравнениям (2.9; 2.11; 2.13) можно строить схему, однако в ряде случаев на практике удобно использовать элементы многоступенчатой логики, однако для этого целесообразно пользоваться методом минимизации ''по нулям''.
Тогда имеем:
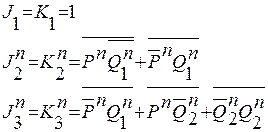 (2.14)
(2.14)
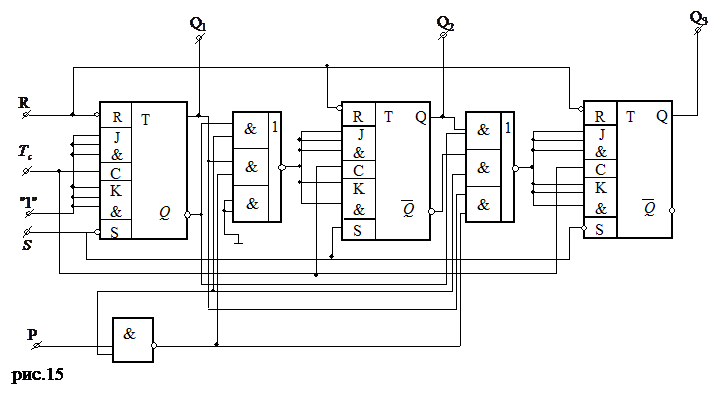
Схема реверсивного счетчика приведена на рис.15
При этом неиспользуемые входы элементов ''2-2-2 И-3 ИЛИ-НЕ'' необходимо подключать к источнику логического нуля, для реализации функции (2.14).
Анализ функционирования реверсивного счетчика аналогичен рис.9, 12 при соответствующих сигналах управления Р.
 2015-02-14
2015-02-14 591
591








