К простым замкнутым сетям относятся кольцевые сети и сети с двухсто-ронним питанием. Кольцевую сеть можно превратить в сеть с двухсторонним питанием, если разрезать ее по источнику питания.
Рассмотрим ЛЭП с двухсторониим питанием (рис. 12.1). Известны:
· мощности нагрузок;
· сопротивления участков ЛЭП;
· напряжения на источниках питания.
Необходимо найти распределение мощностей на участках ЛЭП. Расчет выполним при следующих допущениях:
· в ЛЭП отсетствуют потери мощности;
·
 |
напряжения во всех узлах нагрузок одинаковы и равны номинальному напряжению сети.
Предположим, что нам известна мощность, протекающая на головном участке А-1. Тогда мощности на других участках ЛЭП определяются по I закону Кирхгофа:
S 2 = S 12 = S 1 - S н1;
S 3 = S 23 = S 2 - S н2 = S 1 - S н1 - S н2; (12.1)
S 4 = S 3В = S 3 - S н3 = S 1 - S н1 - S н2 - S н3.
Падение напряжение на любом участке ЛЭП рассчитывается по формуле:
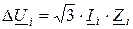 . (12.2)
. (12.2)
Из формулы для расчета мощности на участке ЛЭП (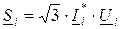 ) найдем ток участка
) найдем ток участка
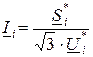
и подставим его в (12.2):
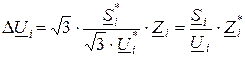 .
.
При учете второго допущения получим:
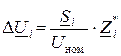 .
.
Найдем падение напряжения во всей ЛЭП:
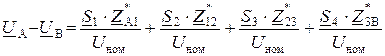
или
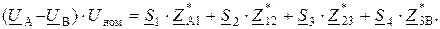
В полученное выражение подставим значения токов участков:
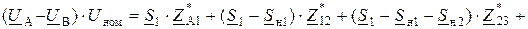
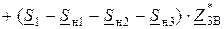 .
.
Выполним преобразования:
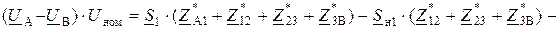
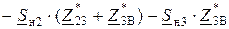 . (12.3)
. (12.3)
Суммы сопротивлений представляют собой сопротивления:

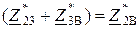 .
.
Выражение (12.3) можем записать следующим образом:
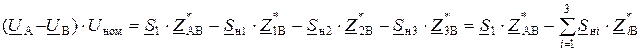 .
.
В полученном выражении только одна неизвестная величина – мощность первого головного участка:
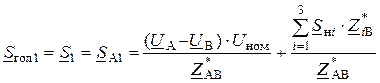 .
.
Если бы мы определяли падение напряжения (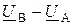 ) и выполнили аналогичные преобразования, то нашли бы мощность второго головного участка:
) и выполнили аналогичные преобразования, то нашли бы мощность второго головного участка:
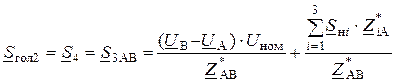 .
.
При n нагрузках:
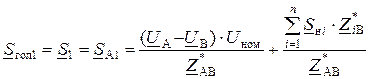 ;
;
(12.4)
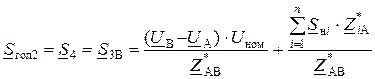 .
.
Правильность полученных расчетов подтверждается выполнением баланса мощности – равенством произведенной и потребленной мощности:
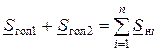 .
.
Мощности на остальных участках определяются по выражениям (12.1).
Значения части мощностей участков получатся отрицательными, т.е. они имеют обратное направление по отношению к принятому. Таким образом, в схеме окажется точка, к которой мощности подходят с двух сторон. Такая точка называется точкой раздела мощности или точкой потокораздела.
Точки раздела активной и реактивной мощности могут не совпадать. Если точки раздела активной и реактивной мощности совпадают, то над этой точкой ставится знак ▼. Если не совпадают, то над точкой раздела активной мощности ставится знак ▼, а над точкой раздела реактивной мощности – знак 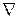 (рис. 12.2).
(рис. 12.2).
 |
В выражениях (12.4) составляющая 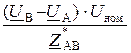 представляет собой уравнительную мощность, протекающую в ЛЭП, из-за разности напряжений на источниках питания. При равенстве напряжений U А = U В (или в кольцевой сети) уравнительная мощность равна нулю.
представляет собой уравнительную мощность, протекающую в ЛЭП, из-за разности напряжений на источниках питания. При равенстве напряжений U А = U В (или в кольцевой сети) уравнительная мощность равна нулю.
Второй член уравнений (12.4) представляет собой сумму моментов нагрузок относительно другого источника питания, разделенную на суммарное сопротивление ЛЭП.
При одинаковых напряжениях на источниках питания очевидно, что падение напряжение от обоих ИП до точки раздела мощности одинаково. Поэтому в этой точке ЛЭП может быть разрезана на два магистральных участка.
При этом нагрузка в конечной точке левого магистрального участка будет равняться мощности, протекающей в исходной сети по первому участку слева от точки потокораздела. Нагрузка в конечной точке правого магистрального участка равняется мощности, протекающей в исходной сети по первому участку справа от точки раздела мощности. Сумма мощностей этих нагрузок должна равняться нагрузке в точке раздела мощности в замкнутой сети (см. рис. 12.3):
S 2 + S 3 = S н2.
 |
Если в схеме две точки раздела мощности, то сеть можно разрезать двумя способами:
· по точке раздела активной мощности (см. рис. 12.4 а). Во всех дальнейших расчетах учитывать знак “минус” перед реактивной мощностью на одном из участков;
· исключить участок между точками раздела мощности (см. рис. 12.4 б). Предварительно следует вычислить потери мощности на участке между точками раздела мощности
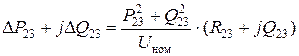
и уточнить мощности нагрузок в точках 2 и 3
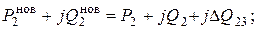
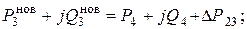
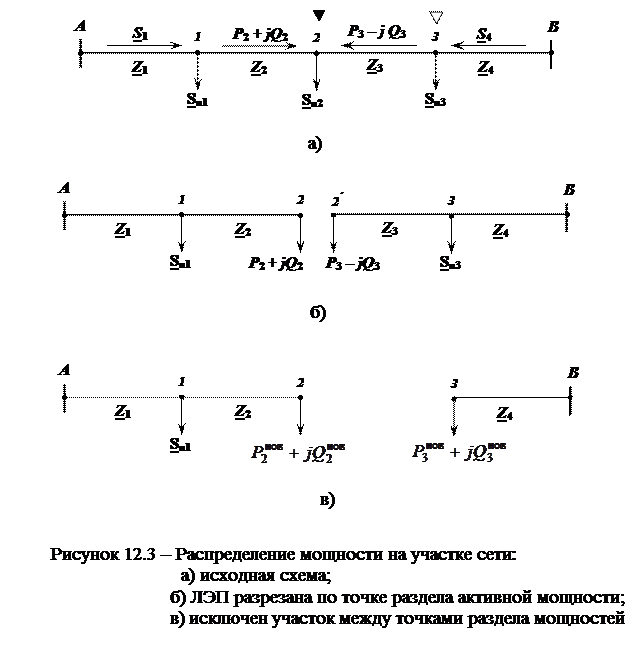 |
В полученных магистралях выполняется расчет режима при заданных напряжениях на ИП, начиная с п. 5 (см. лекцию 9).
 2015-02-14
2015-02-14 737
737








