К исходному дифференциальному уравнению (2) применяется преобразование Лапласа с учетом начальных условий.
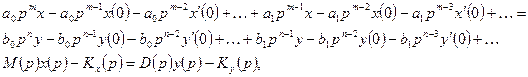
где Kx – это начальное условие по переменной х, Ky – начальное условие по переменной у (а также их производных).
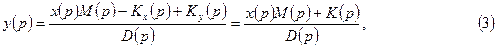
где K(p)=Ky(p)-Kx(p).
1. Применяем прямое преобразование Лапласа к входной величине x(t) (дает х(р)).
2. Получаем в операторном виде переходный процесс по уравнению (3).
3. Используя таблицы Лапласа, осуществляем обратное преобразование Лапласа переменной у(р).
 2015-02-14
2015-02-14 391
391








