Удельная теплоемкость численно равна количеству теплоты, которое нужно сообщить единице массы газа, чтобы увеличить его температуру на 1 градус. Для газа эта величина зависит от условий, при котором происходит нагревание. Можно производить нагревание при постоянном объеме V=const или при постоянном давлении P=const. При нагревании газа при постоянном объеме, все (Q) количество теплоты идет на увеличение внутренней энергии газов
dQ=dU=CvdT
При нагревании газа при постоянном давлении, кроме теплоты идущей на повышение внутренней энергии газа, необходима теплота еще для совершения работы газа на его расширение dA=P·dV. Непосредственное измерение Сp, и особенно, Сv экспериментально затруднительно т.к. теплоемкость газа составит ничтожную долю теплоемкости сосуда, заключающего газ, поэтому измерение будет чрезвычайно неточно. Проще измерить величину: 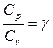 . Это отношение теплоемкости входит в уравнение Пуассона, описывающего адиабатические процессы:
. Это отношение теплоемкости входит в уравнение Пуассона, описывающего адиабатические процессы: 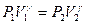 (1)
(1)
Поэтому для определения его предполагается метод адиабатического расширения. Отношение 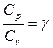 зависит от числа степеней свободы молекул, из которых состоит газ:
зависит от числа степеней свободы молекул, из которых состоит газ:
|
|
|
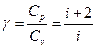
где i –число степеней свободы молекул
Численное значение (i) различно для одноатомных, двух или трех атомных чисел газов, равно соответственно числу степеней свободы, для одноатомного i=3, 2-х атомного i=5, многоатомного i=6. В настоящей работе определяется для воздуха (2-х атомный) i=5.
Метод определения γ, используемый в настоящей работе, основан на законе адиабатического расширения. Процесс, происходящий без теплообмена между системой и средой, называется адиабатическим. В стеклянный баллон при помощи насоса накачивают воздух, создавая внутри баллона давление выше атмосферного. Давление, установившееся в баллоне P1=Н+h1, где H -атмосферное давление, h1 -добавочное давление, измеряемое разностью уровней жидкости в манометре. Таким образом, состояние воздуха внутри баллона, которые назовем I состоянием, характеризуется параметрами: P1=H+h1; V1; T1.
Если открыть на короткое время кран С, то воздух в баллоне будет расширяться. Этот процесс расширения можно назвать адиабатическим. Давление в сосуде установиться равным атмосферному, температура газа понизится до T2. Следовательно в конце адиабатического процесса, называемого II состоянием, параметры будут H; V2; T2.
Применяя к I и II состояниям уравнение (1), получим:
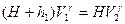 ;
; 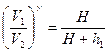 (2)
(2)
Охладившийся при расширении воздух в баллоне через некоторое время вследствие теплообмена нагревается до температуры внешней среды Т, давление возрастает до некоторой величины P2=H+h2 , где h2 - новая разность уровней в манометре, объем воздуха не изменяется и будет равен V2 , т.к. в I и II состояниях воздух имеет одну и ту же температуру (процесс изотермический), то применяя закон Бойля – Мариотта:
|
|
|
P1V1= P2 V2; (H+h1)V1=(H+h2)V2.
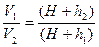 (3)
(3)
возведя обе части уравнения (3) в степень γ;
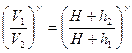 (4)
(4)
пользуясь выражением (2) и (4), получим:
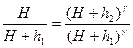 (5)
(5)
логарифмируя последнее выражение и решая относительно γ, получим:
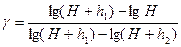 , (6)
, (6)
т.к. давления Н, Н+h1 и Н+h2 мало отличаются друг от друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить:
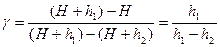 ;
; 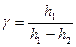 .
.
Таким образом, экспериментальное определение 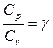 сводится к измерению h1 и h2.
сводится к измерению h1 и h2.
Молярные теплоемкости 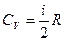 и
и 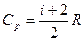 связаны уравнением Майера:
связаны уравнением Майера:
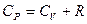 .
.
Удельные теплоемкости: 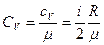 ,
, 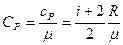 , где μ - молярная масса,
, где μ - молярная масса, 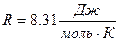 - универсальная газовая постоянная.
- универсальная газовая постоянная.
КОНТРОЛЬНЫЕ ВОПРОСЫ
7. Какое влияние оказывает на результат опыта опоздание при закрытии крана?
8. Почему для газов различают несколько видов теплоемкостей?
9. От чего зависит теплоемкость?
10. Какова связь между удельной и молярной теплоемкостями?
11. Как практически осуществить адиабатический и изотермический процессы? Что это за процессы?
12. Вывести формулу: 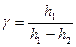 .
.
№4.ЛАБОРАТОРНАЯ РАБОТА
 2015-02-14
2015-02-14 471
471








