2015-02-14
423
8. По данным таблицы 1 по формуле:
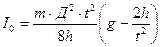(1)
определяют момент инерции маятника без перегрузков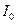 
(в формулу подставляют средние значения измеряемых величин).
9. Затем по данным таблицы по той же формуле (1) определяют момент инерции маятника с перегрузками (тоже через среднее значение).
10. Зная момент инерции маятника с перегрузками и без перегрузков определяют экспериментальный момент инерции самих перегрузков как разность I1э=I1-I0. Экспериментальной момент инерции перегрузков находят и для первого случая, когда расстояние их до оси вращения (R1) и второго случая, с расстоянием до оси вращения (R2).
11. Затем по формуле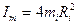 
находят теоретические значения момента инерции перегрузков и для расстояния (R1) и (R2).
12. Сравните значения теоретического значения момента инерция перегрузков и экспериментального соответственно для (R1) и (R2). Выдерживается ли соотношение:
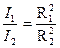4 mi =0,808 кг
13. Сделайте выводы по работе.
14. Ответьте на контрольные вопросы.
Основной закон динамики вращательного движения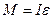 
. Момент инерции 
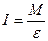. где М – момент силы, ε – угловое ускорение, а – линейное ускорение, Д – диаметр шкива, h – высота падения груза, t – время падения.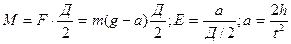 
|
|
|
.
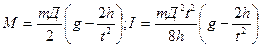КОНТРОЛЬНЫЕ ВОПРОСЫ:
4. Что такое момент инерции и вращающий момент?
5. Основной закон динамики вращательного движения, привести к экспериментальной формуле?
6. Как изменяется момент инерции, если поместить перегрузки ближе к оси вращения?
№ 9 Лабораторная работа
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ
ПОМОЩИ ОБОРОТНОГО МАЯТНИКА (МЕТОД БЕССЕЛЯ)
Для определения ускорения свободного падения пользуются физическим маятником. Физическим маятником называется всякое твердое тело, которое способно совершать колебания под действием силы тяжести вокруг горизонтальной оси не проходящей через центр тяжести.
Ускорение свободного падения можно определить, зная период колебаний физического маятника. Более точно можно произвести это определение с помощью оборотного маятника. Применение оборотного маятника основано на свойстве сопряженности центра качения и точки подвеса.
Это свойство заключается в том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за ту или другую из них, период колебаний его останется тем же. Расстояние между этими точками определяет собой приведенную длину данного маятника.
Если амплитуда колебаний маятника мала, то период колебания его определяется формулой: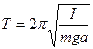 
(1)
где I – момент инерции физического маятника относительно оси вращения;
а – расстояние между осью вращения и центром тяжести маятника;
|
|
|
m – масса маятника.
По теореме Штейнера: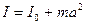 
(2)
где I0 - момент инерции относительно оси, проходящей через центр тяжести и параллельной оси качения.
Пусть маятник качается вокруг оси, проходящей через точку О (рис 1), тогда период его колебаний
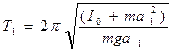(3)
Если маятник подвесить за ось, приходящую через К (рис 2), то его период
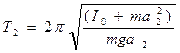(4)
Из формул (3) и (4) имеем:
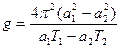(5)
Формулу (5) преобразуем
Умножим числитель и знаменатель на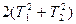 
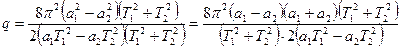
Представим выражение в знаменателе
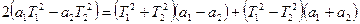
получим: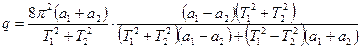 
Заменяя а1+а2=l, где l – расстояние между точками подвеса (ребрами призм) является приведённой длинной физического маятника. Поделив во втором множителе числитель и знаменатель на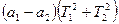 
получим формулу Бесселя:
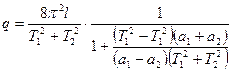(6)
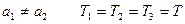
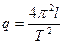(7)
Описание прибора:
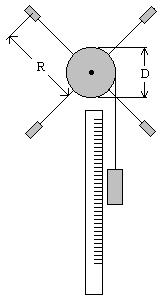
Оборотные маятники в зависимости от предъявленных к ним требований имеют самую различную форму. Они обычно состоят из металлического стержня длиной свыше 1м, на поверхности которого нанесены миллиметровые деления. По стержню могут передвигаться и закрепляться в том или ином положении тяжелые и легкие чечевицы /грузы/ и опорные призмы. Различные комбинации чечевиц и их положений на стержне с опорными призмами дают различные типы оборотных маятников. В настоящей работе применяется оборотный маятник, изображенный на рисунке 3.
На металлическом стержне М опорные призмы А и В жестко закреплены не перемещаются. Жестко закреплена и чечевица С, находящаяся между ними. Вторая чечевица Д находится на конце стержня (не между призмами) и может перемещаться по шкале с нониусом и закрепляется в нужном положении. Расстояние между призмами постоянно.
ВЫПОЛНЕНИЕ РАБОТЫ:
7. Устанавливают чечевицу Д по нониусу в положение 2 см. Отклоняют оборотный маятник на 2-3 см от положения равновесия и отпускают его. Измеряют время 50 полных колебаний и определяют период с точностью до 0, 01с Т=t/50
8. Не меняя точки опоры маятника, передвигают чечевицу в положение 6см и снова измеряют период из 50 колебаний.
9. Те же измерения повторяют для положений 8, 10, 12, 14см.
10. Переворачивают маятник и определяют периоды колебаний при тех же положениях чечевицы, что и в первой опоре. Данные сводят в таблицу.
| Отсчёт по шкале, см. | |||||||
| № 1 (шкала вверх) | |||||||
| № 2 (шкала вниз) |
11. По полученным данным строят графики зависимости периода колебаний маятника от положения чечевицы, откладывая по оси абсцисс деление шкалы, указывающее положение чечевицы, а по оси ординат – величину периода колебаний.
Точка пересечений графиков указывает положение чечевицы, при котором периоды на обоих опорах сравниваются. Это положение определяется по горизонтальной оси в соответствии с масштабом. По вертикальной оси можно оценить приближенное значение общего периода.
12. Устанавливают чечевицу Д по нониусу в положение, взятое с графика с точностью до одного миллиметра. В этом положении определяют точное значение периода, измерив время 100 полных колебаний на той и другой опорах. Т1=t1/100 и Т2=t2/100 с точностью до 0,01с. Для определения величины а1 и а2 маятник снимают с консоли, осторожно кладут его стержнем на специальную подставку, которая имеет острую грань, маятник необходимо уравновесить. Расстояние от точки центра Ц тяжести маятника, находящейся над гранью, до опорных призм дает величины а1 и а. Измерение их производится масштабной линейкой с точностью до миллиметра. По полученным данным, пользуясь формулой Бесселя (7) и вычисляют два значения ускорения свободного падения.
Из двух полученных значений находят среднее, задают доверительную вероятность и вычисляют доверительный интервал. Окончательный результат приводят в виде с доверительной вероятностью.
