Цель работы. Изучение методов численного дифференцирования функций одной переменной.
Задание. 1. Bычислить значение производной в произвольной точке x=x0 аналитически и численно тремя методами для пяти значений приращения аргумента x=1; 0.2; 0.1; 0.01; 0.001. Результаты расчета вывести на экран и распечатать в виде таблицы (табл.3)
Таблица 3
| x | y(x) | y'(x) | 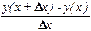
| 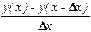
| 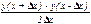
|
| 0.2 | |||||
| 0.1 | |||||
| 0.01 | |||||
| 0.001 |
2. Построить графики функций 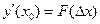 .
.
Варианты функций. Варианты функций приведены в табл.4.
Таблица 4
| Вар. | Вид функции | Вар. | Вид функции |
x(t)=Ae  sin(t+b) sin(t+b)
| y=ctg 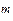 (ax) (ax)
| ||
x(t)=Ae  cos(t+b) cos(t+b)
| y(x)=(e 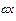 -e -e 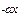 ) ) 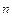
| ||
y(x)=ln 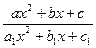
| x(t)=t 
| ||
У(t)=cos 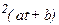
| y(x)=(ax) 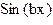
| ||
Y (t)=sin 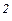 (at+b) (at+b)
| y(x)=arctg 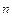 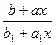
| ||
s()= 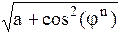
| S(t)= 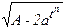
| ||
q(t)=(a-bt 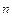 ) ) 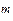
| y(x)=ctg 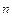 (arcsin ln (arcsin ln 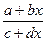 ) )
| ||
y(x)=x 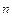 cos(ax) cos(ax)
| R()=arccos 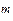 (a+b (a+b 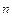 ) )
| ||
y(x)= 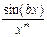
| r()=c 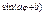
| ||
x(t)= 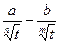
| y(x)=ln(tg 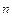 (ax+b)) (ax+b))
| ||
R()= 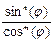
| v(t)=log 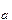 (t (t 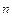 +b +b 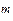 ) ) 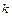
| ||
S()=Вcоs 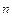 (a+b) (a+b)
| S()=Asin 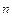 (a+b) (a+b)
| ||
y=tg 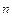 ( (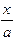 ) )
| x(t)=lg(at  +b) +b)
|
Примечание. Значение параметров a,b,c,d,m,n,A,B выбрать самостоятельно.
Математическое описание. Производная функции определяется как предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной
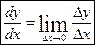 .
.
При численном определении производных заменим отношение бесконечно малых приращений функций и аргумента (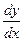 ) отношеним конечных разностей (
) отношеним конечных разностей (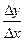 ). Очевидно, что чем меньше будет приращение аргумента, тем точнее численное значение производной. Приращение аргумента будем задавать тремя способами, откладывая x вправо, влево и в обе стороны от исследуемой точки. Соответственно получим три метода численного дифференцирования:
). Очевидно, что чем меньше будет приращение аргумента, тем точнее численное значение производной. Приращение аргумента будем задавать тремя способами, откладывая x вправо, влево и в обе стороны от исследуемой точки. Соответственно получим три метода численного дифференцирования:
метод 1 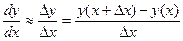 ;
;
метод 2 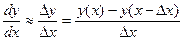 ;
;
метод 3 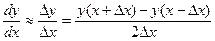 .
.
Суть указанных методов проиллюстрированa на рис.1. Численное значение тангенса угла, образованного касательной к графику y(x) и осью абсцисс, показывает точное значение производной (геометрический смысл производной). Тангенсы углов 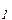 ,
, 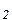 ,
, 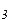 соответствуют численным значениям производных, определенных методами 1,2,3 соответственно (подумайте почему?).
соответствуют численным значениям производных, определенных методами 1,2,3 соответственно (подумайте почему?).
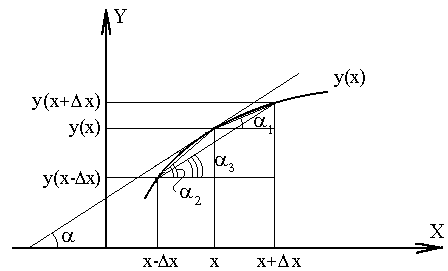 Рис.1.
Рис.1.
Содержание отчета:
1. Название, цель работы и задание.
2. Математическое описание, алгоритм (структограмма) и текст программы.
3. Таблица результатов расчета, четыре графика зависимости 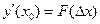 для трех численных методов и точного значения производной, выводы по работе.
для трех численных методов и точного значения производной, выводы по работе.
Лабораторная работа №2
 2015-02-15
2015-02-15 507
507








