Основные законы булевой алгебры

Математический аппарат, описывающий действия цифровых устройств, базируется на алгебре логики, автором которой считается английский математик Дж. Буль (1815–1864 гг.). В практических целях первым применил его американский ученый К. Шеннон в 1938 г. при исследовании электрических цепей с контактными выключателями.

В алгебре логики имеется четыре основных закона:

1. Переместительный, или закон коммутативности для операций сложения и умножения соответственно:

A+B = B+A;

AB = BA.

2. Сочетательный, или закон ассоциативности для сложения и умножения соответственно:

(A + B) +C = A+ (B + C);

(AB) C = A (BC).

3. Распределительный, или закон дистрибутивности для сложения и умножения соответственно:

(A+B) C = AC + BC;

(AB)+ C = (A + C) (B + C).

4. Закон двойственности или инверсии (правило де Моргана) сложения и умножения соответственно:

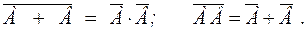
Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей, описываемых законом, или с помощью логических преобразований.

Для преобразований логических выражений пользуются легко доказываемыми тождествами, вытекающими из принципа работы простейших логических элементов (аксиомы алгебры Буля):

Х+ 1=1; Х· 1 =Х; ;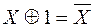

X+ 0 =Х; X ·0=0; X Å0 =Х;

X+X=Х; X·X=Х; X Å X= 0;

; ; .

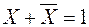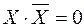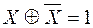С помощью законов алгебры логики и тождеств могут быть доказаны соотношения, получившие названия правил:

поглощения A +AB = A,

A× (A +B) = A

и склеивания

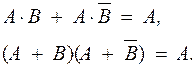
Эти правила широко используют для преобразования переключательных функций с целью их упрощения.

Из правила де Моргана вытекают следствия:

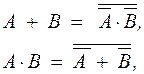
с помощью которых появляется возможность выражать дизъюнкцию через конъюнкцию и отрицание, а конъюнкцию — через дизъюнкцию и отрицание. Законы двойственности справедливы для любого числа переменных.

В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее — конъюнкции, затем — дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок.

Записанная ранее в СДНФ логическая функция трех переменных (3.2) может быть представлена в виде (ей соответствует схема устройства на рис. 3.1, в):

.

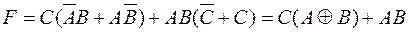Набор логических элементов И, ИЛИ, НЕ называют основным базисом или основной функционально полной системой элементов. Последнее означает, что с помощью этих элементов можно реализовать устройство, осуществляющее сколь угодно сложную логическую операцию. Каждый из элементов И-НЕ и ИЛИ-НЕ также обладает функциональной полнотой.

Базисы И-НЕ и ИЛИ-НЕ называют универсальными. Эти базисы приобрели важное значение в связи с широким использованием интегральных логических элементов при построении логических устройств.

Структуры логических элементов НЕ, И, ИЛИ, построенных из элементов И-НЕ, приведены на рис. 3.3.

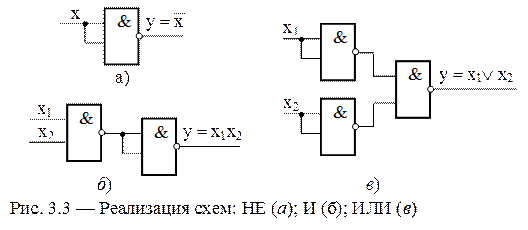
Схема отрицания НЕ реализована на использовании следующего соотношения:

.

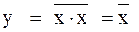Схема логического умножения использует принцип двойной инверсии:

.

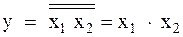Схема логического сложения двух сигналов базируется на использовании закона отрицания:

.

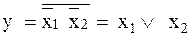Связующим звеном между реальным элементом и его переключательной функцией служит полярность логики. Различают положительную и отрицательную логику. При положительной логике в качестве логической единицы принят высокий уровень сигнала, при отрицательной логике — низкий уровень сигнала. Из принципа дуальности следует, что одно и то же логическое выражение может быть представлено двояко, например,

y = x ₁ x ₂ и .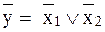

Это значит, что один и тот же элемент будет реализовывать с точки зрения положительной логики функцию конъюнкции, а с точки зрения отрицательой логики — дизъюнкцию.

В дальнейшем в качестве единицы будет принят высокий уровень напряжения (положительная логика).

Минимизация — процесс приведения булевых функций к такому виду, который допускает наиболее простую, с наименьшим числом элементов, физическую реализацию функции. Частная задача минимизации булевой функции сводится к такому представлению заданной функции, которое содержит наименьшее возможное число букв и наименьшее возможное число операций над ними, так как каждой элементарной логической функции соответствует определенный физический элемент.

Оценить различные представления одной и той же булевой функции, например ДНФ, можно по количеству входов логических элементов, реализующих заданную функцию. Для минимизации переключательных функций применяют различные методы: последовательного исключения переменных с помощью законов алгебры логики, с использованием диаграмм Венна, карт Карно (Вейча) и др.