Системой счисления называют способ изображения произвольного числа ограниченным набором символов, называемых цифрами. Номер позиции, определяющий вес, с которым данная цифра складывается в числе, называют разрядом, а системы счисления, обладающие отмеченным свойством, — позиционными.
В общем случае n- разрядное положительное число N в произвольной системе счисления с основанием р представляется суммой вида
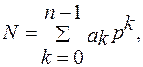 (3.1)
(3.1)
где ak — отдельные цифры в записи числа, значения которых равны членам натурального ряда в диапазоне от 0 до (р – 1).
При выполнении вычислений цифровыми электронными устройствами используются элементы с двумя устойчивыми состояниями. По этой причине в цифровой технике широкое распространение получила позиционная двоичная система счисления (с основанием 2). В каждом двоичном разряде, получившем название бит, может стоять 1 или 0. Сама же запись числа (двоичный код) представляет собой последовательность из единиц и нулей. Чтобы отличить двоичное число от десятичного, будем дополнять его справа суффиксом В (Binary), как это принято в специальных машинно-ориентированных языках программирования, называемых ассемблерами.
Веса соседних разрядов двоичного кода числа отличаются в два раза, а самый правый разряд (младший) имеет вес 1. Поэтому, например
101101 В = 1.25 + 0.24 + 1.23 +1.22 + 0.21 + 1.20 = 45.
Четыре соседних бита называют тетрадой, группу из 8 бит называют байтом, а из 16 бит — машинным словом. Совокупность из 1024 (210) байтов называют килобайтом, из 1024 килобайтов — мегабайтом, из 1024 мегабайтов — гигабайтом.
1 Гб = 210 Мб = 220 Кб = 230 байт.
Современные персональные ЭВМ могут хранить в своей памяти на жестких магнитных дисках цифровую информацию объемом в десятки гигабайтов.
Арифметические операции в двоичной системе счисления исключительно просты и легко реализуются аппаратно. Однако при вводе и выводе информации в цифровое устройство она должна быть представлена в более привычной для человека десятичной системе счисления. Стремление упростить процедуру пересчета двоичных чисел к десятичному эквиваленту привело к использованию двоично-десятичной системы счисления (BD — Binary Decimals). Она используется в ЭВМ не только в качестве вспомогательной системы счисления при вводе и выводе данных, но и в качестве основной при решении задач, когда в ЭВМ вводится и выводится большое количество чисел, а вычислений над ними производится мало. Десятичные числа в двоично-десятич-ной системе счисления кодируются в прямом нормально-взвешенном коде 8-4-2-1, т. е. каждую цифру десятичного числа необходимо заменить соответствующей тетрадой двоичных чисел. Например, десятичное число 9531 в двоично-десятичном коде представляется машинным словом из четырех тетрад
9531 = 1001 0101 0011 0001.
Записывать двоичные числа большой разрядности утомительно. Поэтому, как правило, они представляются более компактными записями с использованием шестнадцатеричной системы счисления. В этой системе используют первые десять членов натурального ряда от 0 до 9, а в качестве остальных цифр — первые шесть латинских букв A = 10, B = 11, C = 12, D = 13, E = 14, F = 15. Справа шестнадцатеричное число будем дополнять суффиксом Н(Hexadecimal).
Перевод двоичного числа в число системы с основанием 16 и наоборот не вызывает затруднений. Для этого исходное двоичное число справа налево разбивается на тетрады, а затем содержимое каждой из них рассматривается как двоичный код соответствующей цифры шестнадцатеричной системы. Для обратного перехода каждую цифру шестнадцатеричного числа заменяют тетрадой двоичного кода, например:
N = 8B5FH = 1000 1011 0101 1111 B.
Таблица 3.1 — Соответствие чисел различных систем счисления
| Десятичное число (D) | Шестнадцатеричное число (H) | Двоичное число (B) |
| A B C D E F |
Для перевода целого числа Np, представленного в системе счисления с основанием р, в систему счисления с основанием q необходимо данное число делить на основание q (по правилам системы с основанием р) до получения целого остатка, меньшего q. Полученное частное снова необходимо разделить на основание q и т. д., пока последнее частное не станет меньше q. Число Nq в новой системе счисления представится в виде упорядоченной последовательности остатков в порядке, обратном их получению. Причем цифру старшего разряда дает последнее частное.
Пример 3.1. Перевести десятичное число 15710 в двоичный код, результат проверить.
| число | делитель остаток |
| 2_____________1 (младший разряд) 2_____________0 2_____________1 2_____________1 2_____________1 2_____________0 15710 = 100111012 2_____________0 2_____________1 (старший разряд) |
Проверка:
100111012 = 1×27 + 0×26 + 0×25 +1×24 + 1×23 + 1×22 + 0×21 + 1×20 =
= 128 + 16 + 8 + 4 +1 =15710.
Для облегчения работы с двоичными кодами желательно знать наизусть десятичные значения чисел 2 n от n = 0 до n = 14 (табл. 3.2).
Таблица 3.2
| n | |||||||||||||||
| 2 n |
Пример 3.2. Перевести десятичное число 15710 в восьмеричный код, результат проверить.
| число | делитель остаток |
| 8_____________5 (младший разряд) 8_____________3 15710 = 2358 8_____________2 (старший разряд) |
Проверка: 2358 = 2×82 + 3×81 + 5×80 = 128 + 24 + 5 = 15710.
Пример 3.3. Перевести десятичное число 15710 в шестнадцатеричный код, результат проверить.
| число | делитель остаток | ||
| 16_____________13 (младший разряд) 16_____________9 (старший разряд) 15710=9D16 | |||
Проверка: 9D16 = 9×161 + 13×160 = 144 + 13 = 15710.
С помощью байта данных можно представить различную информацию:
– целое число без знака (от 0 до 255);
– число от 0 до 99 в двоично-десятичном коде;
– машинный код команд микропроцессора;
– состояние восьми датчиков;
– двоичное число со знаком в прямом, обратном или дополнительном коде ± Х, где Х — модуль числа (от 0 до 127), для отображения которого используется семь младших разрядов. Старший разряд — знаковый (0 — для положительных чисел, 1 — для отрицательных).
|
Прямой, обратный и дополнительный коды положительных чисел совпадают. Для получения дополнительного кода отрицательного числа можно проинвертировать код положительного числа и прибавить единицу. Дополнительный код однобайтового числа минус Х равен дополнению до 256, т. е. двоичному коду числа 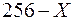 . Преобразование дополнительного кода числа в прямой осуществляется по тому же правилу, что прямого в дополнительный.
. Преобразование дополнительного кода числа в прямой осуществляется по тому же правилу, что прямого в дополнительный.
Пример 3.4. Записать дополнительный код однобайтового числа минус 100. Для отображения знака используется старший разряд числа.
Решение. Запишем двоичный код числа плюс 100: 01100100
Проинвертируем его: 10011011
Прибавим единицу: 10011100
Проверка: 10011100=128+16+8+4=156=256–100.
Ответ: дополнительный код числа минус 100 равен 10011100В.
Таблица истинности
На рис. 3.1, а приведено функциональное обозначение цифрового устройства с тремя входами и одним выходом. Каждый из входных сигналов А, В и С может принимать лишь два значения: 1 и 0. Выходной сигнал F, который можно рассматривать как логическую функцию входных переменных А, В, С, на каждом их наборе может быть равен 1 или 0.
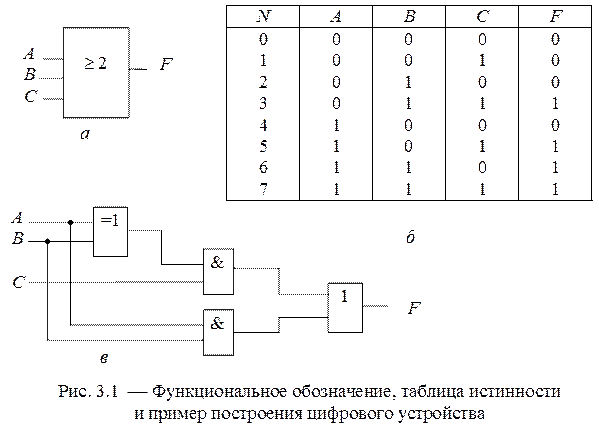
В простейшем случае функция F (A,B,C) может быть задана словесным описанием. Например, функция F равна 1, если все три ее переменные или любая пара из них равны 1, в противном случае F = 0.
Любая логическая функция может быть задана в виде таблицы истинности. На рис. 3.1, б представлена таблица истинности для функции трех переменных, описанной выше словесно. Она определена на восьми наборах, которые располагаются в порядке нарастания десятичного эквивалента N их двоичного кода. В правом столбце указаны значения логической функции F на каждом наборе. Задание логической функции таблицей истинности не всегда удобно, так как при большом числе переменных она становится слишком громоздкой. В этом смысле наиболее привлекателен аналитический способ задания функций в виде так называемых структурных формул, показывающих, какие логические операции необходимо выполнить над входящими в них переменными, чтобы получить значения данной функции.
 2015-02-18
2015-02-18 2049
2049

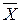 11101111 дополнительный код0, Х 000100001,
11101111 дополнительный код0, Х 000100001, 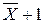 11110000
11110000