В рамках этого метода считают, что известны все внешние силы, включая опорные реакции. Метод основан на интегрировании уравнений равновесия.
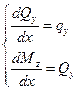 ,
, 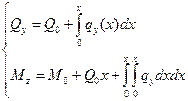 .
.
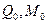 - значения поперечной силы и изгибающего момента в начале стержня. В дальнейшем индексы опустим.
- значения поперечной силы и изгибающего момента в начале стержня. В дальнейшем индексы опустим.
Записанные результаты можно интерпретировать как составление уравнения равновесия участка стержня, заключенного между началом (точка 0) и произвольно выбранным сечением, отстоящим от начала на расстоянии x.
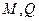 - внутренние силовые факторы.
- внутренние силовые факторы.

1. 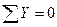 ,
, 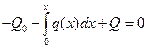 ,
,
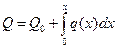 .
.
2. 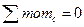 ,
, 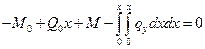 .
.
Удобнее всего рассмотреть применение метода сечений на примере.
Задача:
1. Количество опорных реакций – 3, статических уравнений – 3. Следовательно система статически определима.

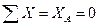 ,
,
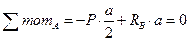 ,
, 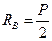 .
.
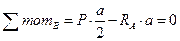 ,
, 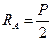 .
.
2. Разделение стержня на участки, внутри которых допускается интегрирование.
Участок 0-1:
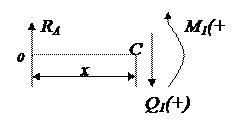
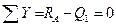 ,
, 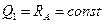 .
.
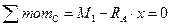 ,
, 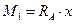 .
.
Участок 1-2:
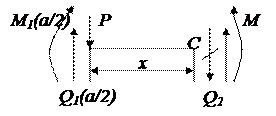
При выделении участка 2 мысленно отбросим участок 1 и его действие на участок 1-2 заменим поперечной силой и изгибающим моментом, вычисленных для конца участка 0-1. проведем сечение на расстоянии x от точки 1 и отбросим все, что находится справа. Действие отброшенного заменим поперечной силой 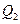 и изгибающего момента
и изгибающего момента 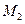 .
.
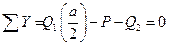 ,
,
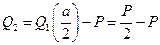 ,
,
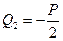 .
.
Необходимо поменять направление 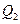 .
.
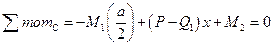 ,
,
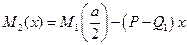 ,
,
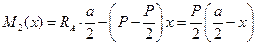 .
.
Задача:

Участок 0-1:
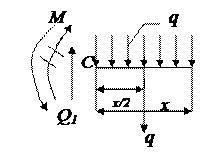
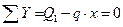 ,
,
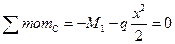 ,
,
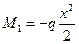 необходимо изменить направление.
необходимо изменить направление.
Участок 1-2:
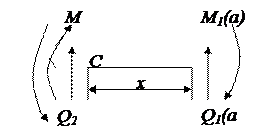
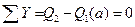 ,
,
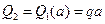 .
.
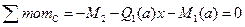 ,
,
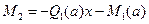 ,
,
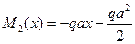 необходимо изменить направление.
необходимо изменить направление.
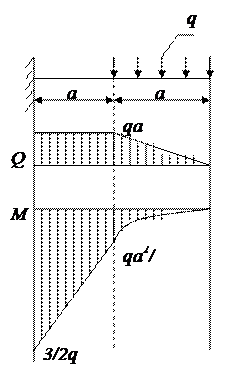
Задача:

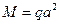 ,
, 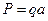 .
.
Так как стержень статически определим, найдем опорные реакции.
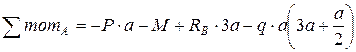
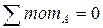
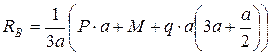
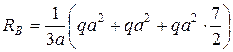
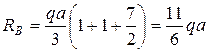
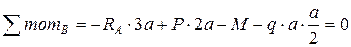
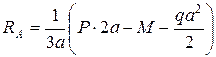
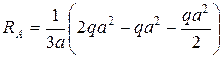
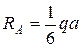
Проверка: 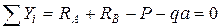
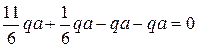
 (верно)
(верно)

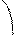


Участок 0 – 1: 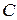
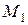

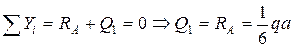
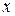





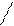

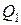
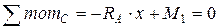
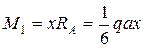
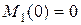
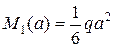


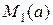
 М
М
 Участок 1 – 2:
Участок 1 – 2: 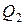
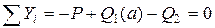





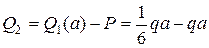
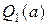
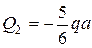
Изменить направление 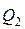 .
.
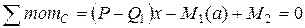
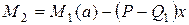
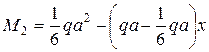
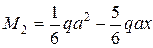
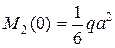
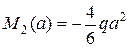
Изменить направление в конце второго участка.
Участок 2 – 3: М М3
 | |||||
 | |||||
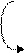 | |||||
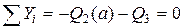
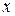

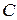
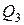
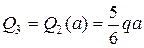
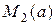
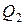
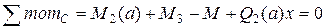
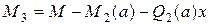
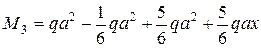
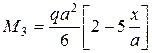
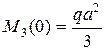
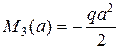
Изменить направление в конце 3-го участка.











 Участок 3 – 4:
Участок 3 – 4:


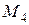

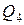
Этот участок будем проходить справа – налево, чтобы аналитическое выражение эпюр было менее сложным.
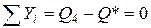
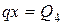
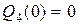
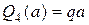
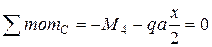
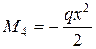
Изменить направление.
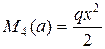
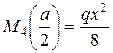
 2015-02-18
2015-02-18 418
418








