Тема 9.2. Корреляционно-регрессионный анализ

Условиями правильного использования методов теории кор­реляции являются следующие:

а) наличие однородности тех единиц, которые подлежат ис­следованию (например, отбор предприятий, которые выпускают однотипную продукцию, имеют одинаковый характер техноло­гии и тип оборудования и т. п.);

б) достаточно большое количество наблюдений, при которых мы погашаем влияние случайностей на результативный признак и имеет силу закон больших чисел;

в) нормальный характер распределения результативного при­знака, на котором построены все положения теории корреляции.

СХЕМА ПОСТРОЕНИЯ УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ

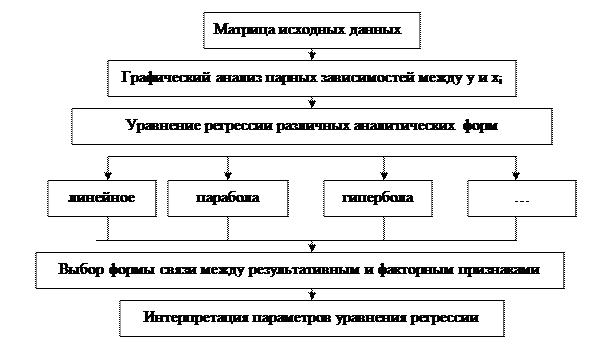
В основе теории корреляции лежит корреляционно-регресси­онный анализ (КРА), суть которого заключается в выборе вида уравнения регрессии

Y=f(x) (1)

В вычислении его параметров и уста­новлении адекватности (соответствия) теоретической зависимос­ти фактическим данным, представленным в табличном фор­ме. Наличие такой теоретической зависимости значительно об­легчает анализ экономических явлений, дает возможность уста­новления прогноза на будущее.

Наиболее часто для характеристики корреляционной связи между признаками применяют такие виды уравнений парной рег­рессии, или корреляционных уравнений:

а) линейный Y = а₀ + a₁ х; (2)

б) параболический Y= a₀ + a_tx² (3)

в) гиперболический Y = а₀ + а₁ /x (4)

г) степенной, Y = а₀ хⁿ и др. (5)
где а_о, a₁— параметры уравнений регрессии, которые подлежат определению.

Параметры a_j. (j=l m) в уравнениях регрессии определя­ются методом наименьших квадратов Уравнение (2) является линейным относительно факторного признака.х и линия регрессии, которая отвечает функции такого вида, будет прямой; уравнения (3) —- (5) — нелинейные и линии регрессии будут соответственно параболой (3), гиперболой (4), степенной линией (5). Соответствующими преобразованиями не­линейные уравнения можно свести к линейной форме, так как клас­сическая теория корреляции является по своей сути линейной.

Этот метод наи­лучшим образом отвечает корреляционной таблице и допускает нахождение таких значений параметров уравнения регрессии, при которых сумма квадратов отклонений табличных (фактических) значений результативного признака у от теоретических значений У по линии регрессии была бы минимальной:

S = ∑(y-Y)² =min,

Функция S параметров уравнения регрессии а_i будет минималь­ной тогда, когда выполняются необходимые условия нахождения экстремума этой функции — равенство нулю первых производ­ных функции по разыскиваемым параметрам:

∂S / ∂a₀ = 0 ∂S / ∂a₁ = 0

Из этих условий формируется система нормальных уравне­ний для нахождения параметров аа и аг

В случае линейного вида уравнения регрессии (2), которое отвечает линейной зависимости между признаками, а система нормальных уравнений записывается в виде:

na₀ + a₁∑x =∑y:

a₀ ∑x_i + a₁∑x² = ∑xy

где n — количество единиц совокупности (то есть заданных пар значений.v и у).

Решив эту систему, находим такие значения параметров:

a₀ = (∑y∑x² - ∑xy∑x) / (n∑x² - ∑x∑x);

a₁ = (n∑yx - ∑y∑x) / (n∑x² - ∑x∑x);

или а_{0 =} y_ср – a₁x_ср; a₁ = ((xy)_ср – x_ср y_ср) / (x_ср ²-(x_ср)²)

Параметр а₁ называется коэффициентом регрессии и показывает изменение результативного признака У при изменении факторного признака х на единицу; геометрически параметр а, отвечает углу наклона (в радианах) прямой линии регрессии к горизонтальной оси.

Для оценки влияния факторного признака на результативный может рассчитываться коэффициент эластичности в среднем для всей совокупности:

К_е = а₁х_ср /y

где х, у - средние величины фактических данных соответствен­но по факторному и результативному признаку в целом для сово­купности.

Коэффициент эластичности показывает, на сколько процен­тов в среднем изменится результативный признак при изменении факторного признака на 1%.

Коэффициент корреляции (корреляционное отношение) пока­зывает, насколько значительным является влияние признака х на Y. Коэффициент корреляции рассчитывается по формуле:

R =√ R²

Он находится в диапазоне 0 < R < 1; чем более близок R к единице, тем теснее корреляционная связь между признаками.

Иногда коэффициент корреляции рассчитывают по формуле, которую можно представить в виде:

R₁ =√∑(1- (y-Y)² / (∑y-ÿ)² )

В случае линейной связи между Y и х величина линейного ко­эффициента корреляции определяется по формуле:

r = ((n∑xy - ∑x∑y) /√ (n∑y²-(∑y)²) 1/(n∑x²-(∑x)².

Значение r лежит в диапазоне -1 = r = +1. При г = 0 не суще­ствует линейной корреляционной связи. Степень тесноты их ли­нейной зависимости растет при приближении к ±1. Когда r > О связь между признаками прямая (при росте х растет У), при r < 0— обратная (при росте х уменьшается Y).

Принято считать, если коэффициент корреляции:

до ±0,3 – связь слабая

±0,3 до ±0,7 – связь средней силы

>± 0,7 связь тесная

После установления тесноты связи дают оценку з начимости связи между признаками. Под термином «значимость связи» по­нимают оценку отклонения выборочных переменных от своих зна­чений в генеральной совокупности посредством статистических критериев. Оценку значимости связи осуществляют с использо­ванием F-критерия. Для парной регрессии (линейной и нелинейной) F-критерий Фишера рассчитывается по формуле:

F =∑(Y - ÿ)² /1: (∑y-Y)² /(n-2)

где [l, (п - 2)] — число степеней свободы числителя и знаменате­ля зависимости.

Вопросы для самоконтроля

1. Дайте определение функциональной, стохастической и корреляционной связи.

2. Дайте определение факторного и результативного признаков.

3. Что означает прямая и обратная связь между признаками?

4. Что показывает коэффициент эластичности?

5. Какие коэффициенты используются для изучения связи качественных признаков?

6. Какие задачи решаются с помощью корреляционно-peгpeccионного анализа?

7. В чем сущность метода наименьших квадратов?

8. В каких пределах изменяется парный (линейный) коэффициент корреляции? Что он показывает?

9. В каких пределах изменяется частный коэффициент регрессии? Что
он показывает?

10. Какой экономический смысл несут свободный член уравнения регрессии и коэффициенты линейного регрессионного уравнения?

11. Линейный коэффициент корреляции может принимать значения …

1. от –1 до +1; 2. от –1 до 0; 3. от –0,5 до +0,5; 4. от 0 до 1.

12. Какое значение коэффициента корреляции показывает наиболее тесную связь?

1. -0,981; 2. -0,957; 3. 0,971; 4. 0,972

13. Коэффициент эластичности показывает …

1. среднее изменение результативного признака при изменении факторного признака на 1%;

2. долю вариации результативного признака под влиянием вариации признака-фактора;

3. направленность корреляционной связи между двумя варьирующими признаками;

4. тесноту связи между двумя варьирующими признаками.

14. Для определения параметров уравнения регрессии можно применять метод

1. наименьших квадратов; 3. скользящей средней;

2. основного массива; 4. параллельных рядов.

ОСНОВНЫЕ ПОНЯТИЯ

Корреляционная связь — изменение среднего значения результатив­ного признака, которое обусловливается изменением факторных приз­наков.

Корреляционное отношение показывает связь между двумя призна­ками.

Корреляция - статистическая зависимость между случайными вели­чинами, которая не имеет строго функционального характера, но измене­ние одной из случайных величин приводит к изменению математическо­го ожидания другой.

Коэффициент детерминации показывает, на сколько процентов ва­риация результативного признака объясняется вариацией j'-го признака (частный) или всех вошедших в модель факторных признаков (множе­ственный).

Коэффициент регрессии показывает, на сколько в среднем изме­няется значение результативного признака при изменении факторного на единицу собственного измерения.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.

Линейная связь - статистическая связь между явлениями, выражен­ная уравнением прямой линии.

Линейный коэффициент корреляции определяет тесноту и направ­ление связи между двумя коррелируемыми признаками.

Нелинейная связь - статистическая связь между социально-эконо­мическими явлениями, аналитически выраженная уравнением кривой линии (параболы, гиперболы и т. д.).

Обратная связь - с увеличением или уменьшением значений фак­торного признака уменьшается или увеличивается значение результатив­ного.

Парная регрессия - аналитическое выражение связи двух признаков.

Прямая связь - с увеличением или уменьшением значений факторно­го признака увеличивается или уменьшается значение результативного.

Ранг - порядковый номер значения признака, расположенного в по­рядке возрастания или убывания величин.

Ранжирование - процедура упорядочения объектов изучения, кото­рая выполняется на основе предпочтения значений признака в порядке возрастания или убывания.

Регрессионный анализ - аналитическое выражение связи, в кото­ром изменение одной величины - результативного признака - обусловле­но влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зави­симую величину, принимается за постоянные и средние значения.

Результативный признак - признак, изменяющийся под действием факторных признаков.

Стохастическая связь - связь, которая проявляется не в каждом от­дельном случае, а в общем, среднем при большом числе наблюдений.

Факторный признак - признак, оказывающий влияние на измене­ние результативного признака.

Функциональная связь - связь, при которой определенному значе­нию факторного признака соответствует одно и только одно значение ре­зультативного признака.