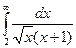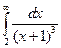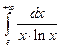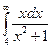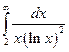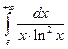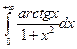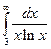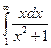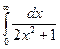Контрольная работа №2
по математическому анализу
(выполняется студентами заочной формы обучения, направление «Экономика» во втором семестре)
Выбор варианта студентом производится по последней цифре (четвертой) зачетной книжки, например, 2284 – вариант № 4; 2280 – вариант №10.
Задание №1.
Найти неопределенные интегралы. Результаты проверить дифференцированием.
1.
а) 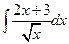
| б) 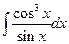
| в) 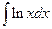
| г) 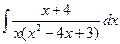
|
2.
а) 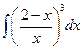
| б) 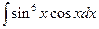
| в) 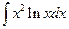
| г) 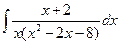
|
3.
а) 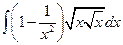
| б) 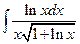
| в) 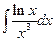
| г) 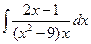
|
4.
а) 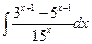
| б) 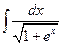
| в) 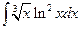
| г) 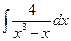
|
5.
а) 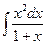
| б) 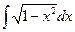
| в) 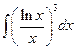
| г) 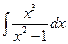
|
6.
а) 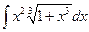
| б) 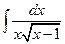
| в) 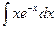
| г) 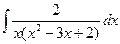
|
7.
а) 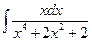
| б) 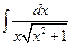
| в) 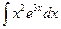
| г) 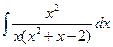
|
8.
а) 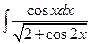
| б) 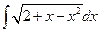
| в) 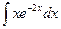
| г) 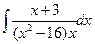
|
9.
а) 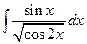
| б) 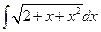
| в) 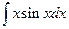
| г) 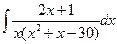
|
10.
а) 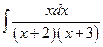
| б) 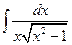
| в) 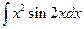
| г) 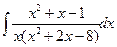
|
Задание №2.
Вычислить площадь фигуры, ограниченной линиями:
1. 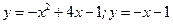
2. 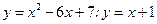
3. 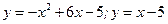
4. 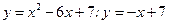
5. 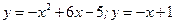
6. 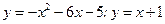
7. 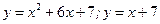
8. 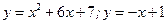
9. 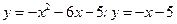
10. 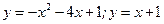
Задание №3.
Вычислить несобственные интегралы или установить их расходимость.
|
Несобственный интеграл первого рода
|
Несобственный интеграл второго рода
1. 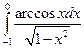 2.
2. 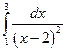 3.
3. 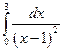 4.
4. 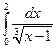 5.
5. 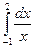 6.
6. 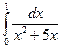 7.
7. 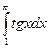 8.
8. 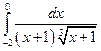 9.
9. 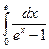 10.
10. 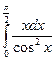
|
Задание №4.
1. Найти среднее значение издержек 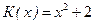 , выраженных в денежных единицах, если объем продукции х изменяется от
, выраженных в денежных единицах, если объем продукции х изменяется от 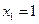 до
до 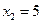 .
.
2. Найти среднее значение издержек 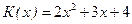 , выраженных в денежных единицах, если объем продукции х изменяется от
, выраженных в денежных единицах, если объем продукции х изменяется от 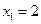 до
до 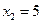 .
.
3. Найти среднее значение издержек 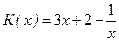 , выраженных в денежных единицах, если объем продукции х изменяется от
, выраженных в денежных единицах, если объем продукции х изменяется от 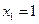 до
до 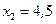 . При каком выпуске продукции издержки равняются найденному среднему значению?
. При каком выпуске продукции издержки равняются найденному среднему значению?
4. Найти среднее значение издержек 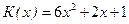 , выраженных в денежных единицах, если объем продукции х изменяется от
, выраженных в денежных единицах, если объем продукции х изменяется от 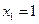 до
до 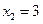 .
.
5. В течение рабочего дня производительность труда меняется по закону 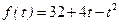 . Сколько продукции будет изготовлено за восьмичасовой рабочий день?
. Сколько продукции будет изготовлено за восьмичасовой рабочий день?
6. В течение рабочего дня производительность труда меняется по закону 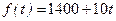 . Сколько продукции будет изготовлено за первые два часа?
. Сколько продукции будет изготовлено за первые два часа?
7. В течение рабочего дня производительность труда меняется по закону 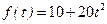 . Сколько продукции будет изготовлено за первый час?
. Сколько продукции будет изготовлено за первый час?
8. В течение рабочего дня производительность труда меняется по закону 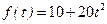 . Сколько продукции будет изготовлено за третий час?
. Сколько продукции будет изготовлено за третий час?
9. В течение рабочего дня производительность труда меняется по закону 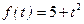 . Сколько продукции будет изготовлено за первых пять часов?
. Сколько продукции будет изготовлено за первых пять часов?
10. Определить объем продукции, произведенной рабочим за пятый час рабочего дня, если производительность труда характеризуется функцией 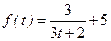 .
.
 2015-03-20
2015-03-20 588
588