В общем случае, как было показано выше, дифференциальные выражения вида:
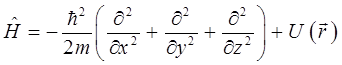
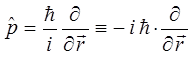
представляют собой частный случай линейных операторов, а функции 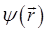 – частный случай векторов
– частный случай векторов 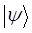 , на которые действуют эти операторы. Так, в квантовой механике каждой динамической переменной – координате, импульсу, угловому моменту (моменту импульса), энергии ставится в соответствие линейный самосопряжённый (эрмитовый) оператор:
, на которые действуют эти операторы. Так, в квантовой механике каждой динамической переменной – координате, импульсу, угловому моменту (моменту импульса), энергии ставится в соответствие линейный самосопряжённый (эрмитовый) оператор:
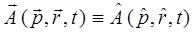
Все функциональные соотношения между величинами, известными из классической механики, в квантовой механике заменяются аналогичными соотношениями между операторами. Соответствие между динамическими переменными (физическими величинами) и квантово-механическими операторами постулируется и является обобщением огромного экспериментального материала. Ранее нами было получено уравнение Шрёдингера (стационарное и нестационарное) из оптико-механической аналогии Гамильтона, на основании рассмотрения задачи о движении частицы в центральном поле сил. Однако математический аппарат и собственно сама аксиоматика квантовой механики может предложить также и другой, операторный путь вывода волнового уравнения Шрёдингера, основанный на свойствах операторов квантовой механики. Так, на основании соответствия между квантово-механическими операторами и динамическими переменными:
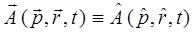
классическое выражение для гамильтониана, имеющее вид:
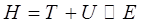
может быть представлено далее к виду:
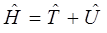
По определению, классическое выражение для кинетической энергии имеет вид:
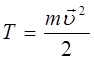
учитывая выражение для импульса:
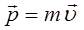
имеем соответственно:
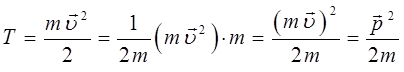
и таким образом:
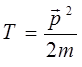
Выражая импульс через его компоненты:
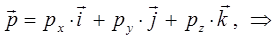
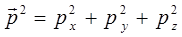
будем иметь соответственно:
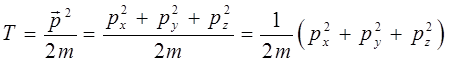
Поскольку, как указывалось уже выше, каждой динамической переменной (физически наблюдаемой величине) в квантовой механике соответствует некоторый линейный самосопряжённый (эрмитовый) оператор, т.е.
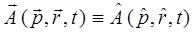
тогда, соответственно классическое выражение для кинетической энергии:
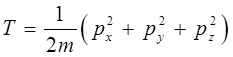
может быть представлено далее к виду:
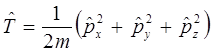
и соответственно для потенциальной энергии:
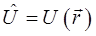
По определению, классическое выражение для импульса имеет вид:
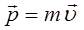
откуда:
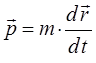
или переходя от векторных к обобщённым величинам, будем иметь соответственно выражение вида:
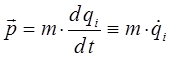
Учитывая, что:
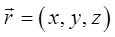
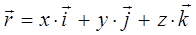
имеем:
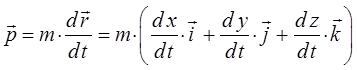
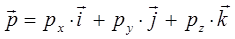
Поскольку любой динамической переменной в квантовой механике ставится в соответствие линейный самосопряжённый (эрмитовый) оператор:
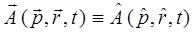
тогда соответственно классическое выражение для импульса, выраженное через его проекции на три неэквивалентных направления в пространстве, могут быть представлены соответственно к виду:
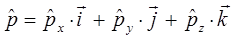
Значение оператора импульса и его компонент можно получить путём решения задачи на собственные значения оператора:
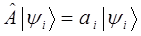
Для этого воспользуемся аналитическим выражением плоской волны де Бройля, полученным нами уже ранее:
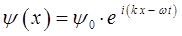
Учитывая, что:
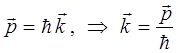
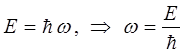
тогда:
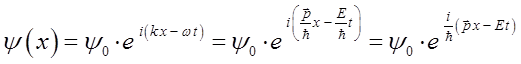
и таким образом:
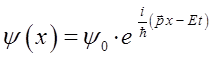
Воспользовавшись уравнением плоской волны де Бройля, решим теперь задачу на собственные значения оператора импульса (его компоненты):
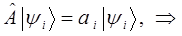
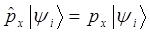
поскольку:
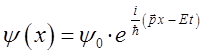
и функция 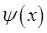 находится по обе стороны операторного уравнения:
находится по обе стороны операторного уравнения:
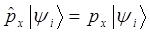
тогда величины амплитуды 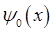 волны сократятся, имеем:
волны сократятся, имеем:
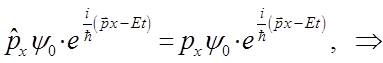
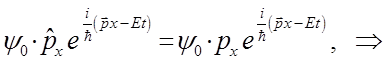
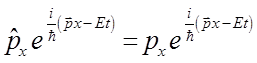
и таким образом формально:
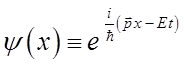
тогда после подстановки в общем виде будем иметь соответственно:
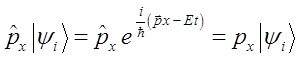
Поскольку оператор компоненты импульса есть дифференциальный оператор, то его действие на волновую функцию как вектор состояния, очевидно, будет сводиться к нахождению производной от этой функции. Тогда решая задачу на собственные значения оператора, приходим к выражению вида:
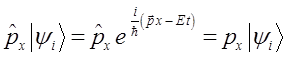
откуда:
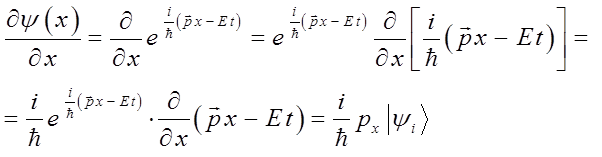
Таким образом, решая задачу на собственные значения оператора, приходим к выражению вида:
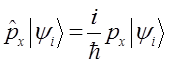
Поскольку, как было выяснено:
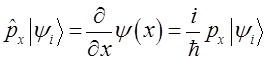
тогда соответственно:
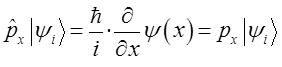
или
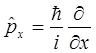
Учитывая, что:
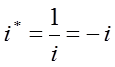
имеем в окончательном виде:
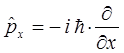
Аналогичным образом можно получить выражения и для двух других компонент оператора импульса, т.е. имеем соответственно:
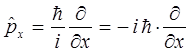
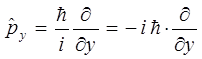
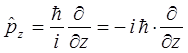
Подставляя полученные выше выражения для компонент оператора импульса в соответствующее выражение для оператора кинетической энергии рассматриваемой системы, будем иметь соответственно:
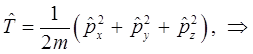
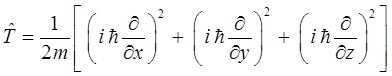
и таким образом, после подстановки соответствующих выражений для операторов компонент импульса, получаем:
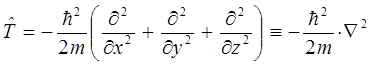
учитывая также, что:
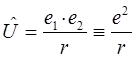
имеем соответственно:
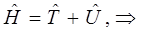
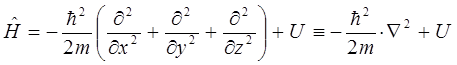
Необходимо, однако, отметить, что само по себе данное выражение лишено смысла, поскольку операторы представляют собой просто определённые математические действия, преобразующие исходные функции (вектора) – оригиналы в их линейные отображения. По этой причине будет логично, если оператор полной энергии системы (гамильтониан) будет действовать на некоторую функцию, содержащую в себе всю возможную информацию о свойствах системы частиц и определяющую таким образом всё, что только может быть известно о квантово-механической системе. Такую функцию в квантовой механике называют волновой функцией. Она полностью описывает состояние частицы (системы частиц) в любой момент времени. Учитывая всё выше сказанное, а также исходя из операторного уравнения, являющегося аналитическим выражением задачи на собственные значения оператора, будем иметь соответственно:
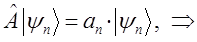
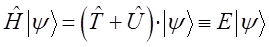
или после соответствующих подстановок, приходим к уравнению вида:
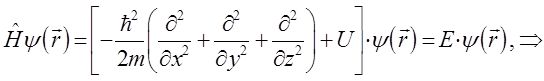
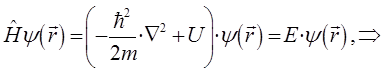
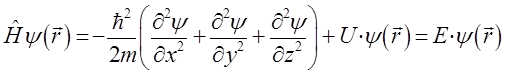
или что то же самое:
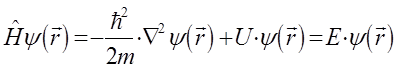
представляя его далее к виду:
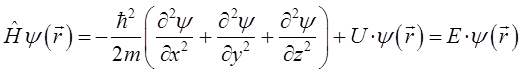
получим:
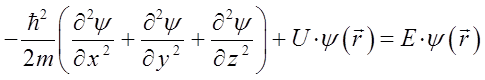
откуда соответственно:
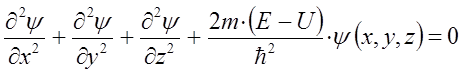
 2015-03-22
2015-03-22 531
531








