Методика обработки результатов прямых измерений

Теперь мы можем приступить к изучению элементарных правил обработки экспериментальных данных. Начнём с самой простой и одновременно важнейшей методики обработки результатов прямых измерений.

Обозначим через 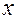измеряемую физическую величину. Пусть в результате нескольких опытов получено n пронумерованных значений 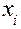(i – номер измерения, i = 1,2,3,…,n). Зададимся вопросом: Какую ошибку 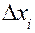мы допустили в каждом отдельном измерении? При известном истинном значение 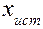, решение очевидно .

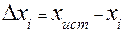Поскольку, 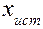нам не доступно, то его заменяют средним значением 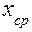, которое легко найти по известной формуле.

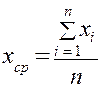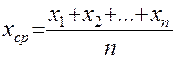или . (1)

Тогда, ошибка отдельного измерения (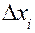) (несмотря на неизбежную небольшую неточность этих вычислений) легко вычисляется

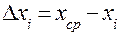(2)

Зная ошибку каждого измерения, следующим шагом найдем, так называемое среднеквадратическое отклонение среднего :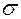

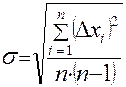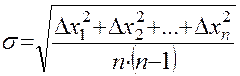или . (3)

(Внимание! Среднеквадратическое отклонение среднего 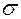вычисляют с точностью 10%-20%, не более 2 значащих цифр)

Формула для вычисления 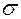доказывается в теории вероятности! Для практических целей существенное значение имеет её смысловое наполнение. Отложим на оси всевозможных 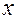, значения, , , .

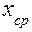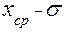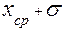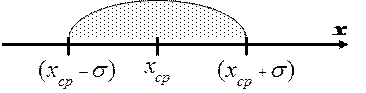Оказывается, что при проведении новых серий экспериментов, следующие средние значения 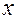будут попадать в интервал от (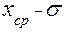) до (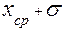) примерно 68 раз из 100. С точки зрения теории вероятности можно утверждать, что истинное значение 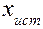лежит в интервале 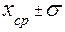с вероятностью 68%.

Вероятность 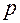, с которой среднее значение попадает в некоторый интервал, называется доверительной вероятностью, при этом интервал называют доверительным интервалом .

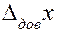Однако 68% невысокая вероятность. В подавляющем большинстве случаев требуется знать интервал 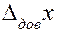с доверительной вероятностью 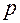= 90%, 95%, 98%. Найти его очень просто, если известны 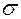и специальные коэффициенты Стьюдента 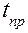, зависящие от числа измерений 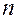и доверительной вероятности .

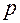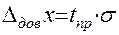(4)

Обработка случайных погрешностей прямых измерений сводится к нахождению 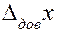с заданной доверительной вероятностью.

В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым 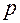= 0,95.

Таблица коэффициентов Стьюдента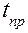

для доверительной вероятности 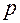= 0,95

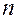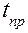	12,3	4,3	3,18	2,78	2,6	2,26

Полная погрешность измерений 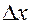складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу:

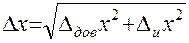(5)

Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:

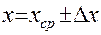, (6)

Рядом необходимо указать относительную погрешность

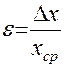, (7)

выраженную в процентах (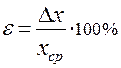) (8)

Внимание, относительная погрешность ε превышающая 10%-15% свидетельствует о недостаточном усердии учащегося при выполнении лабораторной работы.

Заметим, что 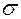и, следовательно, 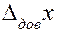вычисляют с точностью порядка 10%–20%. Поэтому при вычислении полной ошибки удобно пользоваться следующим правилом: если одна из ошибок 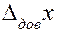или 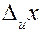превышает другую в 3 и более раз, то меньшей можно пренебречь.

Пример 2: Пусть 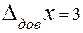; 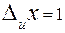, тогда: .

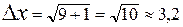Пренебрегая 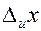, получим .

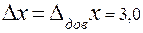Определим относительную ошибку, которую мы совершаем, пренебрегая :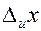

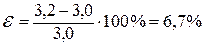, следовательно, действие допустимо.

Пример 3, когда инструментальная погрешность превышает случайный разброс 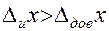. При измерении штангельцуркулем диаметра шариков подшипника были получены следующие результаты: 13,2мм; 13,1мм; 13,2мм; 13,1мм; 13,1мм; 13,1мм. Очевидно, что все измеренные значения лежат внутри интервалов 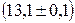мм или 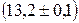мм. Инструментальная погрешность отдельного измерения 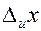в данном случае 0,1мм (цена деления). В этом случае бессмысленно считать среднее значение и находить 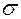, любая из двух записей будет правильным результатом, а полная ошибка равна инструментальной 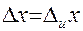(легко проверить 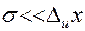). Причина в том, что случайные изменения диаметра слишком малы по сравнению с погрешностью штангельцуркуля.

Отметим также, что в случае однократных измерений вычисление 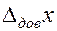бессмысленно. В этом случае полную погрешность принимают равной инструментальной .

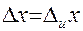§2