Билеты коллоквиума

Билет № 1

1. Дайте частотное определение вероятности случайного события. Какое событие называется достоверным? Приведите примеры.

2. Что называется моделью материального тела? Приведите примеры идеальных квантовых моделей. Как определяются микроскопические состояния таких систем?

3. Какова вероятность того, что в объеме, составляющем одну треть объема, предоставленного молю идеального газа, содержится две трети моля вещества?

4. Распределение плотности вероятности некоторой случайной величины х имеет вид 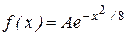. Определите А и s (х) без использования процедур интегрирования.

5. Запишите распределение Гиббса (непрерывное и дискретное), условие нормировки для него.

6. Рассчитайте флуктуацию энергии системы, если её среднее значение

< E > = NkT ².

Билет № 2

1. Определите понятия:

• микроканонический ансамбль систем;

• канонический ансамбль систем.

2. Сформулируйте статистические постулаты.

3. Докажите, что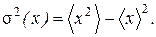

4. Что называется плотностью вероятности? Поясните с помощью графика.

5. Выведите формулу для расчета 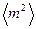с помощью биномиального распределения Р(т).

6. Что называется статистической суммой? Какая связь между статсуммой и нормировочной постоянной А распределения Гиббса?

Билет № 3

1. Чем определяется микроскопическое состояние системы:

а) если применима классическая модель материального тела; б) если применима квантовая модель материального тела.

2. Сколько статистических постулатов Вы знаете? Дайте их краткую формулировку.

3. Как определяется относительная величина флуктуации? Чему она равна в случае биномиального распределения?

4. Определите предельные случаи биномиального распределения. Какие явления они описывают? Приведите примеры.

5. Выведите распределение Гиббса.

6. Как рассчитать флуктуацию энергии системы, если известно, что средняя энергия системы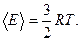

Билет № 4

1. Как определяется вероятность случайного события с помощью понятия «ансамбль систем»?

2. Какой факт отражает условие нормировки плотности вероятности?

3. Какова вероятность того, что в объеме, составляющем одну сотую часть объема, предоставленного молю идеального газа, содержится полмоля вещества?

4. Чему равна относительная величина флуктуации в случае распределения Пуассона?

5. На какой вопрос отвечает распределение Гиббса?

6. Запишите выражение для средней энергии частицы через статистическую сумму.

Билет № 5

1. В рамках статистического методаопределите состояниетермодинамического равновесия системы.

2. Как определяется среднее значение случайной величины (дискретной и непрерывной)?

3. Исследуйте выражение для дисперсии числачастиц в объёме v в случаебиномиального распределения, если объём v много меньше всего объёма системы.

4. Докажите, что биномиальное распределение отвечает условию нормировки.

5. Как определяется температура в статистике?

6. Получите общее выражение для 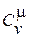через одночастичную статистическую сумму идеальной системы.

Билет № 6

1. Что называется термодинамической вероятностью макроскопического состояния системы?

2. Что называется флуктуацией случайной величины?

3. Выведите формулу длярасчета 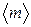с помощью биномиального распределения Р(т).

4. Сравните распределения Гаусса и Пуассона. К описанию каких явлений они применимы? Приведите примеры.

5. Что называется кратностью вырождения состояния или его статистическим весом? Какая величина является его аналогом в случае непрерывного распределения?

6. Получите выражение для расчета дисперсии энергии s (Е) на основе статистической суммы.

Билет № 7

1. Как определяется вероятность макроскопического состояния системы? Поясните на примере распределения Гиббса.

2. Что называется условием нормировки вероятностей? Каков ее смысл?

3. Выделите основные признаки явлений, которые описывает биномиальное распределение? Запишите его вид.

4. Как определяется параметр b в распределении Гиббса? Почему b > 0?

5. Определите область применимости распределения Гиббса.

6. Как рассчитать s(Е), если известно, что средняя энергия системы 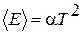, а = const.

Билет № 8

1. Для чего подсчитывают микроскопические состояния в статистике? Приведите пример, как это делают при выводе биномиального распределения.

2. Как определяется вероятность случайного события «по времени» и «по ансамблю»?

3. Чему равна наиболее вероятная концентрация частиц в некотором объеме v, являющемся частью большого объема V газовой системы, распределение молекул в которой описывается законом Бернулли?

4. Чему равна дисперсия случайной величины в распределении Пуассона?

5. Какую информацию можно получить с помощью формулы, определяющей температуру в статистике?

6. Запишите статистическую сумму двухуровневой системы и среднюю энергию одной частицы этой системы, если кратность вырождения состояния с меньшей энергией равна 4, а с большей − 6.

Билет № 9

1. Что называют микроскопическими состояниями системы? Как и зачем их подсчитывают?

2. Какое достоверное событие лежит в основе нормировки плотности вероятности?

3. Сформулируйте статистические постулаты.

4. Как рассчитать среднее число частиц в объеме v, если полный объем системы 10 v? Силовых полей нет. Система – идеальный классический газ.

5. Выведите распределение Гиббса.

6. Как рассчитать среднюю энергию системы на основе статистической суммы?