2015-03-22
495
Данные задачи относятся к теме «Элементы линейной и векторной алгебры». Ознакомьтесь со следующими вопросами по этой теме:
1. Определители n-го порядка, их свойства и вычисление. Миноры и алгебраические дополнения.
Определитель n-го порядка имеет вид:
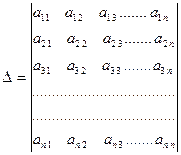(1)
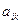- элементы определителя, при этом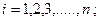 
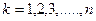
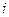- номер строки, 
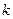- номер столбца, на пересечении которых находится элемент 
.
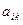Определение1. Минором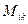 
элемента 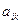определителя (1) называется определитель (n-1)-го порядка, полученный путем вычеркивания 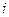-ый строки и 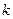-ого столбца.
Определение 2. Алгебраическим дополнением (адъюнктом) элемента 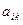определителя (1) называется произведение минора 
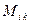этого элемента на множитель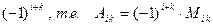 
Определение 3. Определителем (детерминантом) n-го порядка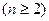 
называется число, равное сумме произведений элементов первой строки на их алгебраические дополнения, т.е.
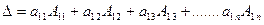(2)
Запись по формуле (2) называется разложением определителя (1) по элементам первой строки. Определение позволяет вычислить определитель, понижая его порядок последовательно до определителя второго порядка вида:
|
|
|
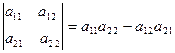
С помощью свойств определитель можно разложить по элементам любой строки и любого столбца и в любой строке (столбце) вместо элементов, кроме одного, можно получить элементы равные нулю. Это облегчит вычисление определителя. Этого можно достичь, используя очень важное свойство:
величина определителя не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число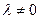 
.
2.Решение систем линейных уравнений по формулам Крамера, методом Гаусса.
Дана система трех линейных уравнений с тремя неизвестными:
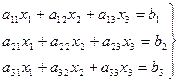(1)
Формулы Крамера имеют вид: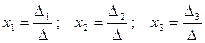 
, где определитель системы 
составлен из коэффициентов при неизвестных, т.е.
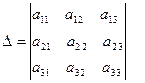определители 
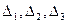составлены из определителя 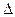системы уравнений (1)
путем замены соответственно первого, второго и третьего столбца столбцом из свободных членов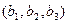 
.
Метод Гаусса состоит в последовательном исключении неизвестных. Для этого выбираем, например, первое уравнение за «ведущее». Из второго и третьего уравнения системы (1) вычитаем «ведущее», умноженное соответственно на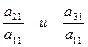 
. В итоге во втором и третьем уравнении члены, содержащие неизвестное 
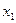, будут исключены. Система примет вид:
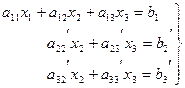(2)
Аналогично, выбрав второе уравнение за «ведущее», исключаем неизвестные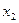 
из уравнения системы уравнений (2). Система примет вид:
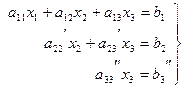(3)
Из третьего уравнения системы (3) найдем неизвестные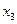 
, из второго - 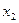, а из первого уравнения - .
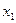Замечание. Системы линейных уравнений (1), (2) и (3) эквивалентны.
3. Линейно зависимые и независимые векторы. Ранг и базис системы векторов. Разложение вектора по единичному и произвольному базису.
|
|
|
Система векторов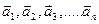 
(1) линейно зависима, если равенство 
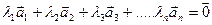выполняется при условии, что хотя бы один из коэффициентов разложения 
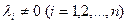. Если же это равенство выполняется при условии, когда все 
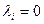, то векторы линейно независимы.
Определение 1. Рангом n мерного пространства называется максимальное число линейно независимых векторов этого пространства.
Определение 2. Любая система n линейно независимых векторов n – мерного пространства называется базисом этого пространства.
Из этого определения и теоремы о линейной независимости n векторов n – мерного пространства следует, что любая система n – мерных векторов образует базис n – мерного пространства, если определитель, составленный из координат, не равен нулю.
Например, единичные векторы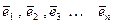 
n – мерного пространства образуют единичный базис.
Замечание. Ранг n – мерного пространства совпадает с размерностью пространства.
4. Матрицы, виды матриц. Действия над матрицами. Ранг матрицы. Обратная матрица и ее вычисление.
Матрицей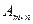 
называется таблица, т.е.
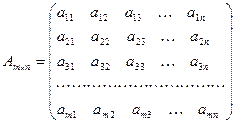
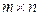- размерность матрицы, m – число строк, n – число столбцов в матрице.
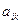- элементы матрицы,
i = 1,2,3 … m
k = 1,2,3 … n
Замечание. Матрица – это таблица, и смешивать ее с определителем нельзя!
Строки и столбцы матрицы можно рассматривать соответственно как n – мерные векторы и m – мерные векторы.
Определение 1. Минором r – го порядка матрицы (1) называется определитель r – го порядка, составленный из элементов, стоящих на пересечении любых r строк и r столбцов.
Определение 2. Рангом матрицы называется наивысший порядок ее минора, отличного от нуля.
Определение 3. Рангом матрицы называется максимальные числа линейно независимых векторов – строк и векторов – столбцов.
Обозначается r (A)
Даны матрицы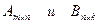 
Определение 4. Произведением матриц 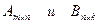называется матрица 
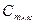, элементы 
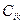которой равны сумме произведений элементов i – ой строки матрицы 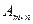на соответствующие элементы k- го столбца матрицы 
.
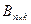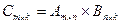
Замечание. Произведение матриц существует, если число столбцов матрицы A равно числу строк матрицы В.
Пусть дана квадратная матрица
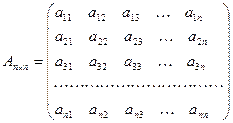
Определение 5. Квадратная матрица n – порядка называется неособенной (невыраженной), если её ранг равен n, т.е. определитель матрицы n – го порядка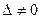 
.
Определение 6. Матрица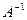 
называется обратной матрицей для данной квадратной матрицы А, если выполняются условия:
А · 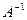= E и 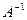· А = Е, где
E – единичная матрица
Обратная матрица вычисляется по формуле
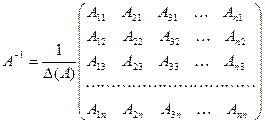,где
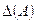– определитель матрицы
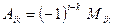- алгебраические дополнения элементов определителя.
5. Матричная запись системы линейных уравнений и её решение с помощью обратной матрицы.
Систему n линейных уравнений с n неизвестными
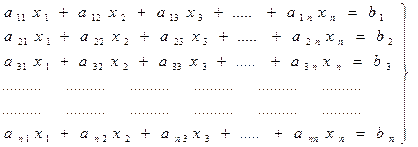
можно записать в матричной форме:
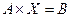, где A – матрица, составленная из коэффициентов при неизвестных, X матрица – столбец, составленная из неизвестных и B матрица – столбец, составленная из свободных членов.
Умножим равенство 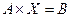слева направо на 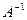, получим 
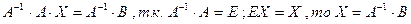- формула для решения системы уравнений с помощью обратной матрицы.
Рассмотрим задачи.
Задача 1. Даны матрицы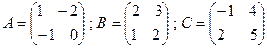 
. Найти матрицу D=(2A-3B)C и вычислить её определитель.
Решение. При умножении числа на матрицу нужно это число умножить на каждый элемент матрицы,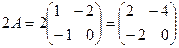 
. Аналогично, найдем произведение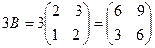 
При вычитании матриц получим матрицу, элементы которой равны разностям соответствующих элементов матриц 2А и 3В, т.е.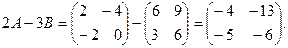 
Для нахождения произведения используем правило умножения матриц. (см. п. 4 определение 4)
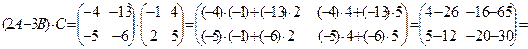
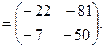
Определители второго порядка вычисляются по формуле: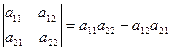 
.
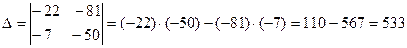Задача 2. Выяснить, существует ли для данной матрицы А обратная матрица.
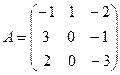
Решение. Обратная матрица вычисляется по формуле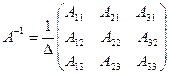 
,
где 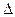- определитель матрицы А, т.е. 
.
|
|
|
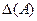Вычисляем определитель матрицы А:
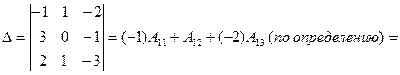
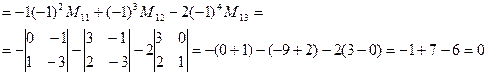
Обратная матрица не существует.
Задача 3. Найти матрицу, обратную для данной матрицы А. Сделать проверку.
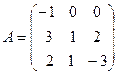
Решение. Обратная матрица вычисляется по формуле 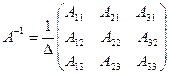(1)
где 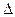- определитель матрицы А. Вычислим определитель.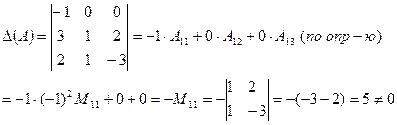 
Т.к. определитель матрицы не равен нулю, то обратная матрица существует.
Вычислим алгебраические дополнения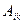 
по формуле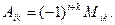 
.
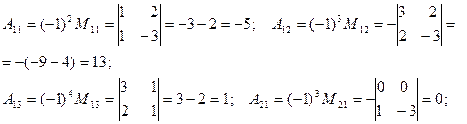
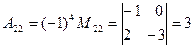
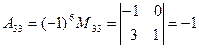Найденные значения определителя и алгебраических дополнений подставим в формулу (1).
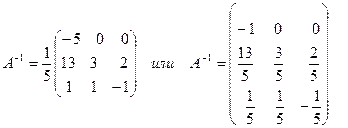
Для того чтобы проверить, правильно ли найдена обратная матрица, нужно использовать определение, т.е. проверить, выполняются ли равенства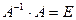 
; 
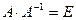. Найдем произведение 
:
= 
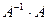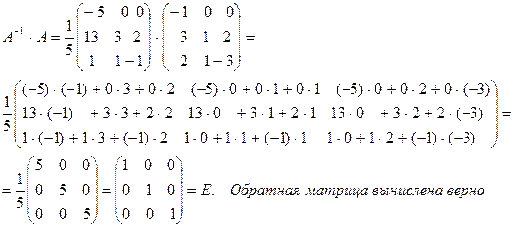
Внимание! Найдите произведение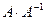 
.
Задача 4. Данную систему линейных уравнений решить методом Гаусса и матричным методом (с помощью обратной матрицы).
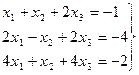(1)
Решение. I Для системы уравнений (1) выберем за «ведущее» первое уравнение и будем исключать неизвестное 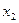из второго и третьего уравнений. Для этого к левой и правой частям второго уравнения прибавить соответственно левую и правую части первого «ведущего» уравнения, а из левой и правой части третьего уравнения вычесть соответственно левую и правую части первого уравнения. Система уравнений примет вид:
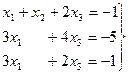(2)
В полученной системе уравнений (2) за «ведущее» уравнение примем второе уравнение и исключим неизвестное 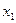из третьего уравнения. Для этого из левой и правой частей третьего уравнения вычтем соответственно левую и правую части второго уравнения.
Система уравнений (2) примет вид:
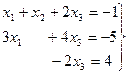
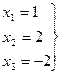
II Для решения с помощью обратной матрицы запишем систему уравнений (1) в матричной форме, введя матрицы A,X,B. Матрица A составляется из коэффициентов при неизвестных, Х – матрица – столбец из неизвестных, В – матрица – столбец из свободных членов.
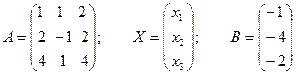
Тогда система уравнений примет вид: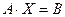 
. Умножив равенство слева направо на обратную матрицу 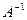получим:
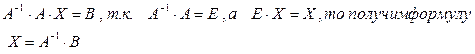
Вычислим обратную матрицу по формуле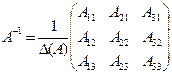 
(см. решение предыдущей задачи).
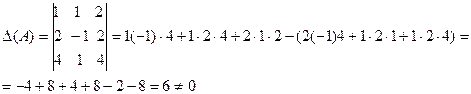
- обратная матрица существует. (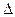 вычислен по правилу треугольника).
|
|
|
Вычислим алгебраические дополнения по формуле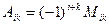 
.
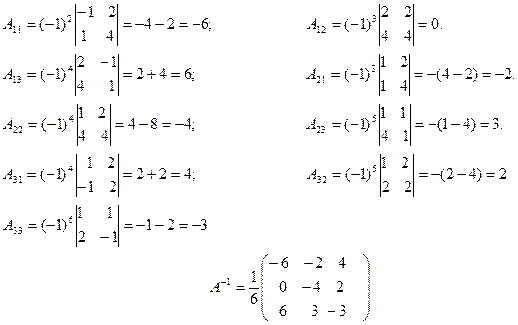
Найдем матрицу Х:
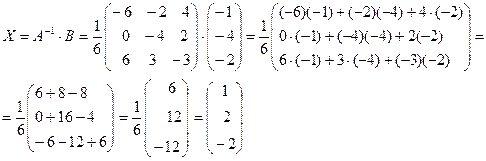
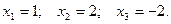
Проверка. В данную систему уравнений вместо неизвестных подставить найденные значения.
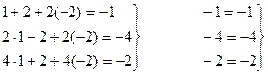
Система решена верно, т.к. получили три тождества.
Задача 5. Даны векторы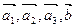 
. Показать, что векторы 
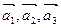образуют базис трехмерного пространства и найти координаты вектора 
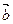в этом базисе.
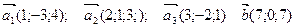
Решение. 1. Векторы образуют базис, если они линейно независимы. Три вектора в трехмерном пространстве линейно независимы, если определитель, составленный из координат этих векторов не равен нулю.
Составим и вычислим определитель третьего порядка и вычислим его по правилу треугольника.
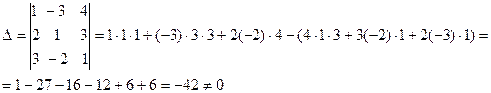
Т.к. определитель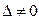 
, то векторы 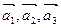образуют базис.
2. Запишем разложение вектора 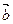по этому базису (или представим вектор 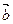в виде линейной комбинации векторов базиса)
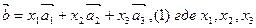- неизвестные коэффициенты разложения, подлежащие определению.
Запишем векторное уравнение (1) в координатной форме:
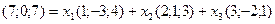(2)
От уравнения (2)перейдем к системе трех линейных уравнений с тремя неизвестными. Для этого используем правило умножения числа на вектор, правило сложения векторов и условие равенства векторов в координатной форме.
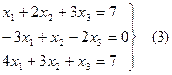
Примем первое уравнение за «ведущее» и исключим неизвестное 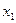, из второго и третьего уравнений. Для этого ко второму и третьему уравнению прибавим первое, умноженное соответственно на 3 и (-4). Получим эквивалентную систему уравнений вида:
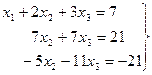(4)
Будем исключать неизвестное 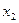. Для этого левую и правую части второго уравнения разделим на 7, а затем к третьему уравнению прибавим второе, умноженное на 5.
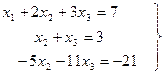
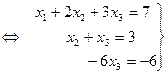
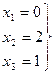
Из третьего уравнения найдем 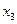. Подставим значение 
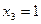во второе уравнение последней системы и найдем 
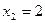. Значение 
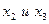подставим в первое уравнение и найдем 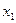. Найденные значения коэффициентов разложения подставим в равенство (1) и получим разложение вектора 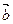по базису векторов .
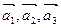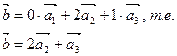
Координаты вектора 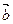в новом базисе: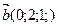 
Замечание. Чтобы проверить – правильно ли решена система уравнений (3), нужно найденные значения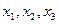 
подставить в каждое уравнение системы. Если каждое уравнение обратится в тождество, то система решена верно.
