Названные задачи относятся к теме «Дифференциальные уравнения». По этой теме необходимо изучить следующие вопросы:
1. Какое уравнение называется дифференциальным? Как определяется порядок дифференциального уравнения?
Определение. Уравнение, связывающее независимую переменную 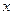 , искомую функцию
, искомую функцию 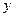 и ее производные, называется дифферен-циальным.
и ее производные, называется дифферен-циальным.
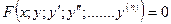 или
или
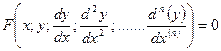
Порядок дифференциального уравнения определяется наличием наивысшей производной:
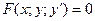 - дифференциальное уравнение первого порядка
- дифференциальное уравнение первого порядка
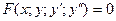 - дифференциальное уравнение второго порядка
- дифференциальное уравнение второго порядка
2. Что называется решением дифференциального уравнения? Общее и частные решения дифференциальных уравнений первого и второго порядка.
Определение. Решением дифференциального уравнения называется такая функция 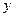 , которая вместе с ее производными удовлетворяет этому уравнению (превращает его в тождество).
, которая вместе с ее производными удовлетворяет этому уравнению (превращает его в тождество).
Общее решение имеет вид: 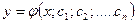 .
.
Решение, полученное из общего при конкретных значениях произвольных постоянных 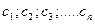 называется частным.
называется частным.
Общее решение дифференциальных уравнений первого и второго порядка имеют соответственно вид:
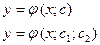
3. Задача Коши для дифференциального уравнения первого и второго порядков.
Задача отыскания частного решения дифференциального уравнения, удовлетворяющего начальным условиям:
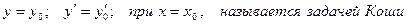
4. Дифференциальное уравнение первого порядка с разделяющимися переменными: 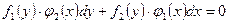 . Нахождение их общего и частного решений.
. Нахождение их общего и частного решений.
Дифференциальные уравнения первого порядка с разделяющимися переменными 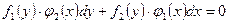 сводится к уравнению с разделенными переменными
сводится к уравнению с разделенными переменными 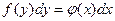 , которое решается интегрированием обеих частей:
, которое решается интегрированием обеих частей:
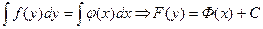
5. Линейное дифференциальное уравнение первого порядка: 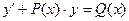 Отыскание его общего и частного решений.
Отыскание его общего и частного решений.
Линейные дифференциальные уравнения первого порядка 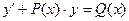
при 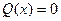 является уравнением с разделяющимися переменными. Если
является уравнением с разделяющимися переменными. Если 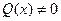 , то уравнение решается с помощью подстановки
, то уравнение решается с помощью подстановки 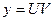 ,где
,где 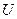 и
и 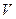 неизвестные функции, зависимые от
неизвестные функции, зависимые от 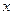 . После ряда преобразований линейное уравнение сводится к двум дифференциальным уравнениям с разделяющимися переменными.
. После ряда преобразований линейное уравнение сводится к двум дифференциальным уравнениям с разделяющимися переменными.
6. Линейные однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, нахождение их общих и частных решений.
Задача. Найти общее решение дифференциального уравнения 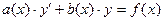 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию 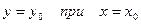
Уравнения предлагаемого вида являются линейными, так как содержат искомую функцию «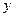 » и ее производную «
» и ее производную «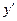 » в первых степенях. Один из способов решения таких уравнений заключается в том, что функцию y(x) ищем в виде произведения двух дифференцируемых функций u(x) и v(x), одна из которых подбирается специальным образом, а другая находится из условия их удовлетворения исходному уравнению. С помощью этого приема решение линейного дифференциального уравнения первого порядка сводится к решению двух дифференциальных уравнений с разделяющимися переменными соответственно для функций u(x) и v(x).
» в первых степенях. Один из способов решения таких уравнений заключается в том, что функцию y(x) ищем в виде произведения двух дифференцируемых функций u(x) и v(x), одна из которых подбирается специальным образом, а другая находится из условия их удовлетворения исходному уравнению. С помощью этого приема решение линейного дифференциального уравнения первого порядка сводится к решению двух дифференциальных уравнений с разделяющимися переменными соответственно для функций u(x) и v(x).
Рассмотрим ряд примеров. Напомним, что производная равна отношению дифференциалов:
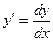
Пример 1. 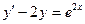 ;
; 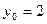 при
при 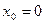 .
.
Ищем решение уравнения в виде 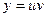 . Найдем производную этого произведения:
. Найдем производную этого произведения: 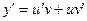 . Подставим функцию y и ее производную
. Подставим функцию y и ее производную 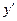 в исходное уравнение:
в исходное уравнение:
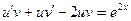
В левой части уравнения сгруппируем слагаемые, имеющие общий множитель «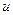 », и вынесем его за скобку:
», и вынесем его за скобку:
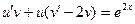
Подберем вспомогательную функцию «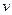 » так, чтобы обратилось в нуль выражение, стоящее в круглых скобках:
» так, чтобы обратилось в нуль выражение, стоящее в круглых скобках:
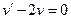 (1)
(1)
Тогда уравнение примет вид:
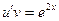 (2)
(2)
Оба последних уравнения решаются разделением переменных.
Сначала находим частное решение первого из них, то есть функцию 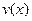 , а затем, подставив ее во второе уравнение, найдем функцию
, а затем, подставив ее во второе уравнение, найдем функцию 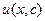 .
.
1) 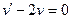 ;
; 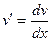 2)
2) 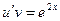
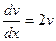 ;
; 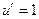
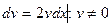 ;
; 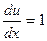
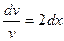 ;
; 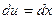
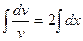 ;
; 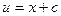
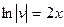
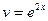
Замечание. Решая первое уравнение (для вспомогательной функ-ции 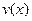 ), берем лишь его частное решение, соответствующее
), берем лишь его частное решение, соответствующее 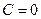 . При решении второго уравнения для функции
. При решении второго уравнения для функции 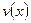 находим общее решение уравнения.
находим общее решение уравнения.
Так как 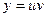 , то
, то 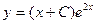 - общее решение уравнения.
- общее решение уравнения.
Для нахождения частного решения обратимся к начальному условию: 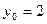 при
при 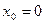 . Подставим эти значения в найденное общее решение дифференциального уравнения:
. Подставим эти значения в найденное общее решение дифференциального уравнения:
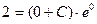 ,
,
так как 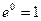 , то
, то 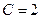
Подставим найденное значение С в общее решение дифференциального уравнения, получим его частное решение:
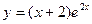 .
.
Ответ: 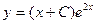 - общее решение дифференциального уравнения;
- общее решение дифференциального уравнения;
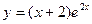 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Пример 2. 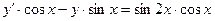 ;
; 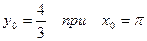
Ищем решение в виде 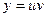
Найдем производную: 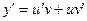 .
.
Подставим в исходное уравнение 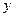 и
и 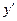 :
:
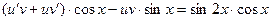 ;
; 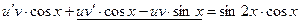
Сгруппируем подчеркнутые слагаемые, вынеся за скобку общий множитель u:
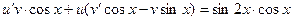
Подберем вспомогательную функцию 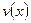 из условия:
из условия:
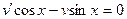 (1)
(1)
Тогда уравнение примет вид:
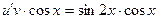 (2)
(2)
Решаем поочередно два последних уравнения, причем для первого из них берем лишь частное решение 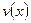 , соответствующее
, соответствующее 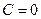 .
.
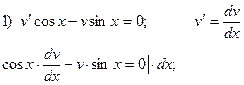
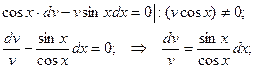
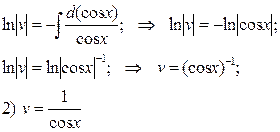
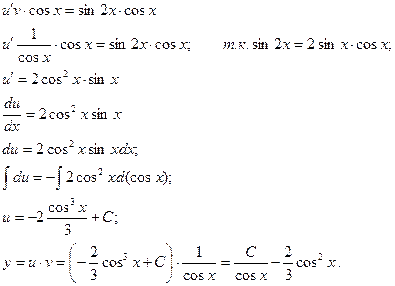
Таким образом, 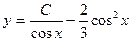 - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Для нахождения частного решения воспользуемся начальными условиями: 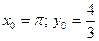 , подставив их в найденное общее решение:
, подставив их в найденное общее решение:
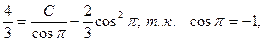
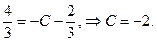
Подставим 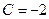 , в общее решение уравнения:
, в общее решение уравнения:
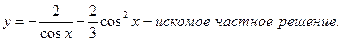
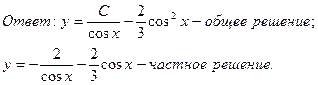
Пример 3. 
Ищем решение в виде 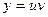 , тогда
, тогда 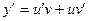 .
.
Подставим 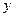 и
и 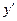 в данное уравнение:
в данное уравнение:
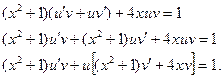
Потребуем, чтобы 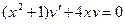 (1), тогда
(1), тогда 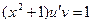 (2)
(2)
Решим последовательно оба уравнения, причем для первого из них берем лишь частное решение при 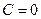 .
.
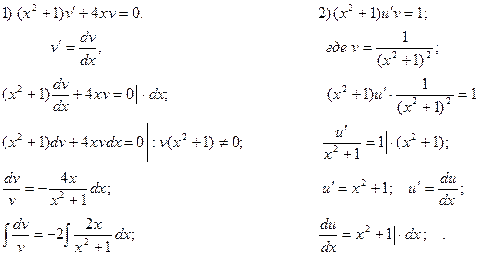

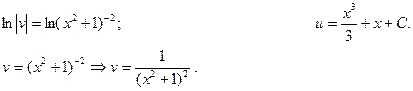
Так как 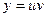 , то
, то
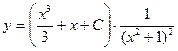 - это общее решение исходного дифферен-
- это общее решение исходного дифферен-
циального уравнения.
Для нахождения частного решения обратимся к начальным условиям 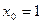 ;
; 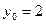 и подставим их в найденное общее решение:
и подставим их в найденное общее решение:
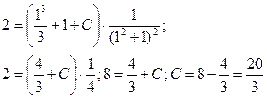
Искомое частное решение получим из общего, подставив в него найденное значение 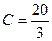 :
: 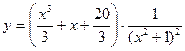
Ответ: 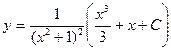 - общее решение;
- общее решение;
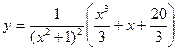 - частное решение.
- частное решение.
Замечание. Чтобы проверить правильность найденного решения (общего или частного), нужно подставить его в исходное уравнение и убедиться, что получится верное равенство (тождество).
Пример 4. Найти частное решение уравнения:
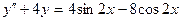 ,
,
удовлетворяющее начальным условиям 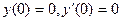 .
.
Решение. Общее решение 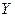 данного уравнения равно сумме общего решения
данного уравнения равно сумме общего решения 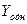 однородного уравнения и какого-либо частного решения
однородного уравнения и какого-либо частного решения 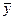 данного уравнения, то есть
данного уравнения, то есть
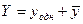
Для нахождения 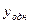 составим характеристическое уравнение
составим характеристическое уравнение 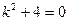 , имеющее комплексные корни
, имеющее комплексные корни 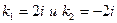 . В этом случае общее решение однородного уравнения ищем в виде
. В этом случае общее решение однородного уравнения ищем в виде
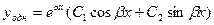 (4)
(4)
где 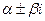 - комплексные корни характеристического уравнения. Подставим в (4)
- комплексные корни характеристического уравнения. Подставим в (4) 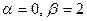 , имеем:
, имеем:
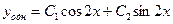
Для нахождения частного решения 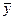 неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция 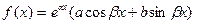 и числа
и числа 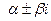 не являются корнями характеристического уравнения, то существует частное решение
не являются корнями характеристического уравнения, то существует частное решение 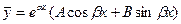 . Если же числа
. Если же числа 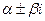 являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение 
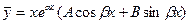 .
.
Применяя эту теорему при 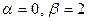 , имеем:
, имеем:
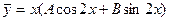 .
.
Дважды дифференцируя последнее равенство, находим 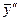 :
:
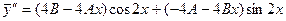
Подставив в данное уравнение 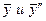 , получим:
, получим:
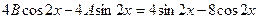 ,
,
Откуда 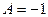 ,
, 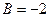 .
.
Следовательно, 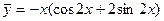 и
и
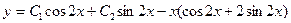
Найдем 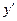 :
:
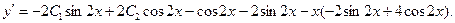
Используя начальные условия, получим систему
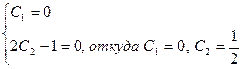
Следовательно, 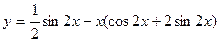 есть искомое частное решение данного дифференциального уравнения.
есть искомое частное решение данного дифференциального уравнения.
 2015-03-22
2015-03-22 824
824








