ЗАДАЧИ
1.5. Найти число инверсий в перестановках:
1) 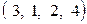 ; ; | 3) 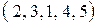 ; ; | 5) 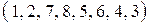 . . |
2) 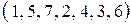 ; ; | 4) 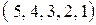 ; ; |
Миноры и их алгебраические дополнения
Пусть дана прямоугольная матрица 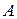 размера
размера 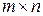 , и пусть
, и пусть 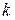 – целое положительное число такое, что
– целое положительное число такое, что 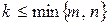 . Выберем
. Выберем 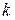 строк и
строк и 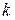 столбцов в матрице
столбцов в матрице 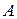 соответственно с номерами
соответственно с номерами 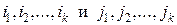 , причем эти номера расположены по возрастанию:
, причем эти номера расположены по возрастанию:
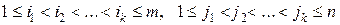 .
.
Определение 3.1. Определитель 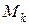 порядка
порядка 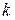 , составленный из элементов матрицы А, расположенных на пересечениях выбранных строк и столбцов, называется минором
, составленный из элементов матрицы А, расположенных на пересечениях выбранных строк и столбцов, называется минором 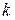 -го порядка матрицы
-го порядка матрицы 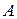 :
:
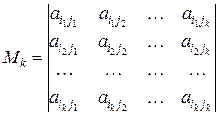 . (3.1)
. (3.1)
Миноров 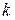 -го порядка у матрицы
-го порядка у матрицы 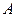 размера
размера 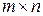 столько, сколько имеется возможностей выбрать
столько, сколько имеется возможностей выбрать 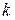 различных строк и
различных строк и 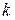 различных столбцов, то есть
различных столбцов, то есть
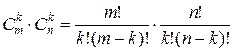 .
.
Например, пусть дана 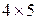 - матрица и пусть
- матрица и пусть 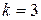 . Выберем три строки и три столбца, например, с номерами
. Выберем три строки и три столбца, например, с номерами 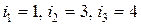 и
и 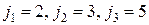 соответственно. Определитель третьего порядка
соответственно. Определитель третьего порядка
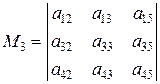 ,
,
составленный из элементов матрицы 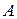 , расположенных на пересечениях выбранных строк и столбцов, является одним из миноров третьего порядка матрицы
, расположенных на пересечениях выбранных строк и столбцов, является одним из миноров третьего порядка матрицы 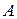 . Их число равно
. Их число равно
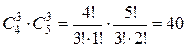 .
.
Пусть 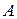 – квадратная матрица порядка
– квадратная матрица порядка 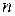 , и пусть
, и пусть 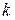 – целое положительное число, меньшее
– целое положительное число, меньшее 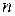 . Пусть
. Пусть 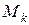 есть некоторый минор вида (3.1) матрицы
есть некоторый минор вида (3.1) матрицы 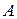 . Вычеркнем в
. Вычеркнем в 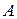 строки и столбцы, на пересечениях которых расположены элементы минора
строки и столбцы, на пересечениях которых расположены элементы минора 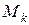 . Оставшиеся невычеркнутыми элементы образуют матрицу порядка
. Оставшиеся невычеркнутыми элементы образуют матрицу порядка 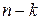 . Определитель этой матрицы (обозначим его символом
. Определитель этой матрицы (обозначим его символом 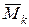 ) называется дополнительным минором к минору
) называется дополнительным минором к минору 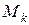 , а число
, а число 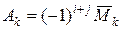 , где
, где 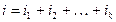 ,
, 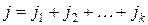 – алгебраическим дополнением минора
– алгебраическим дополнением минора 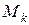 .
.
Каждый элемент 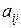 матрицы
матрицы 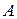 можно рассматривать в качестве минора первого порядка. Если
можно рассматривать в качестве минора первого порядка. Если 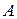 – квадратная матрица и
– квадратная матрица и 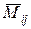 – дополнительный минор к
– дополнительный минор к 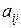 , то число
, то число 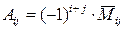 является алгебраическим дополнением элемента
является алгебраическим дополнением элемента 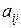 .
.
Пример 1. Найти алгебраические дополнения элементов второй строки матрицы
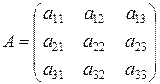 .
.
Решение. Вычеркнем в матрице  вторую строку и первый столбец. Оставшиеся невычеркнутыми элементы образуют матрицу второго порядка, определитель которой
вторую строку и первый столбец. Оставшиеся невычеркнутыми элементы образуют матрицу второго порядка, определитель которой
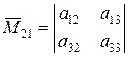
является дополнительным минором к элементу 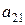 . Вычеркивая второй, а затем третий столбцы, аналогично получаем дополнительные миноры к элементам
. Вычеркивая второй, а затем третий столбцы, аналогично получаем дополнительные миноры к элементам 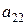 и
и 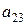 :
:
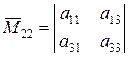 ,
, 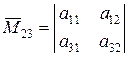 .
.
Полагая в формуле
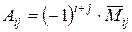
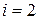 и
и 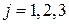 , находим алгебраические дополнения элементов второй строки матрицы
, находим алгебраические дополнения элементов второй строки матрицы 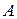 :
:
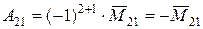 ,
, 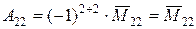 ,
, 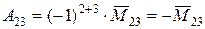 .
.
Теорема 3.1 (теорема разложения). Сумма произведений элементов любой 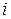 - й строки (любого
- й строки (любого 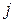 -го столбца) определителя на соответствующие алгебраические дополнения элементов этой строки (этого столбца) равна этому определителю:
-го столбца) определителя на соответствующие алгебраические дополнения элементов этой строки (этого столбца) равна этому определителю:
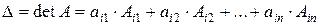 , (3.2)
, (3.2)
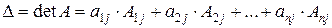 . (3.3)
. (3.3)
Формулы (3.2) и (3.3) называются формулами разложения определителя 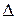 по элементам
по элементам 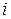 -й строки и
-й строки и 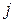 -го столбца соответственно.
-го столбца соответственно.
Эти формулы можно записать соответственно в форме:
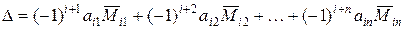 ; (3.4)
; (3.4)
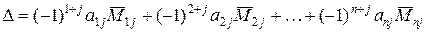 , (3.5)
, (3.5)
в которой они обычно и употребляются.
Пример 2. Разложить определитель
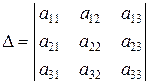
по элементам второй строки.
Решение. Полагая в формуле (3.4) 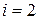 и
и 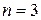 , получаем (см. пример 1)
, получаем (см. пример 1)
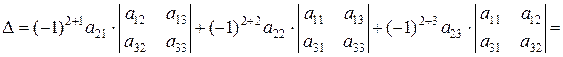
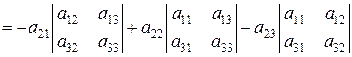 .
.
Пример 3. Вычислить определитель
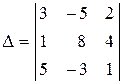 ,
,
разлагая его по элементам второго столбца.
Решение.
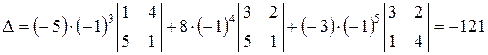 .
.
Пример 4. Вычислить треугольный определитель 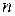 -го порядка
-го порядка
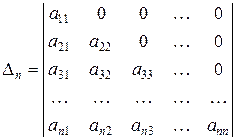 .
.
Решение. Разлагая 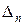 по первой строке, получаем
по первой строке, получаем
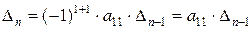 ,
,
где
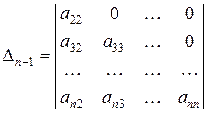 .
.
Разлагая снова по первой строке уже треугольный определитель 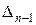 , получаем
, получаем
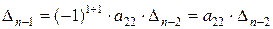 ,
,
где 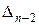 – треугольный определитель
– треугольный определитель 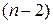 -го порядка.
-го порядка.
Продолжая таким образом далее, окончательно получаем
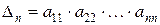 ,
,
то есть треугольный определитель равен произведению элементов, стоящих на его главной диагонали.
Пример 5. Вычислить определитель
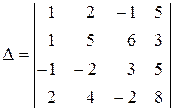 ,
,
путем приведения его к треугольному виду.
Решение. Воспользовавшись свойством 8 определителя (см. § 2), приведём данный определитель к треугольному виду. Для этого из второй строки вычтем первую, к третьей строке прибавим первую, из четвертой строки вычтем первую, умноженную на 2. Получим
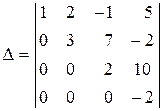 .
.
Так как определитель треугольного вида равен произведению элементов главной диагонали (см. пример 4), то
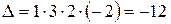 .
.
Замечание. По теореме разложения определитель порядка n выражается через n определителей (n – 1)-го порядка. Однако целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов (строке или столбце) все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведётся к одному определителю более низкого порядка. Указанное преобразование определителя можно выполнить, опираясь на его свойства.
Пример 6. Вычислить определитель
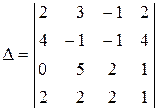 .
.
Решение. Из второй строки вычтем первую, а из четвертой – третью. При таких преобразованиях величина определителя не изменится (см. § 2, свойство 8). Следовательно,
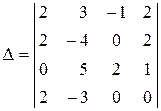 .
.
Прибавив к элементам третьей строки соответствующие элементы первой строки, умноженные на 2, получим
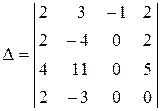 .
.
Разлагая этот определитель по элементам третьего столбца (см. формулу (3.5)), находим
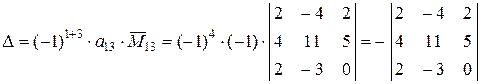 .
.
Вычтем из первого столбца третий, а затем прибавим к третьей строке вторую, умноженную на 2:
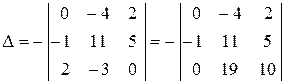 .
.
Разложив определитель по элементам первого столбца, найдём
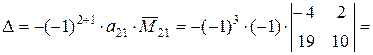
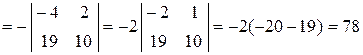 .
.
Теорема 3.2 (теорема аннулирования). Сумма произведений элементов какого-либо ряда (строки или столбца) определителя на алгебраические дополнения соответствующих элементов любого другого параллельного ряда равна нулю.
Утверждение теоремы 3.2 выражается равенствами:
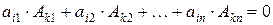 при
при 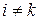 , (3.6)
, (3.6)
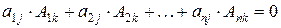 при
при 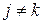 , (3.7)
, (3.7)
где 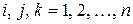 .
.
Например, для определителя
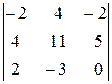
сумма попарных произведений элементов второй строки и алгебраических дополнений соответствующих элементов первой строки равна нулю:
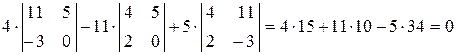 ,
,
что соответствует утверждению теоремы 3.2, то есть формуле (3.6).
Для формулы (3.7) аналогичным подтверждением является равенство нулю суммы произведений, например, элементов первого столбца на алгебраические дополнения соответствующих элементов третьего столбца рассматриваемого определителя:
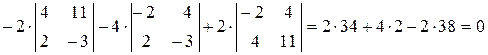 .
.
ЗАДАЧИ
1.6. Вычислить определители по правилу треугольников:
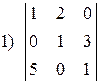 ; ; | 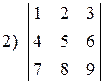 ; ; | 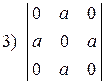 . . |
1.7. Предварительно преобразовав определитель, вычислить его, используя формулы (3.2) и (3.3):
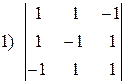 ; ; | 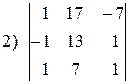 ; ; | 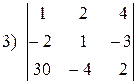 ; ; | 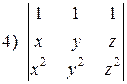 . . |
 2015-03-22
2015-03-22 1502
1502







