Пусть  – квадратная матрица
– квадратная матрица 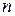 -го порядка, а
-го порядка, а 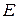 – единичная матрица того же порядка.
– единичная матрица того же порядка.
Матрица 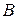 называется правой обратной по отношению к матрице
называется правой обратной по отношению к матрице  , если
, если 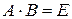 . Если же
. Если же 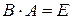 , то
, то 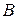 называется левой обратной к матрице
называется левой обратной к матрице  . Ясно, что
. Ясно, что 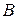 является квадратной матрицей порядка
является квадратной матрицей порядка 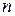 .
.
Теорема 4.1. Если у квадратной матрицы  существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
Доказательство. Пусть матрицы 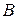 и
и 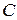 такие, что
такие, что
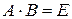 и
и 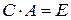 .
.
Тогда 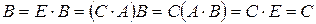 . ■
. ■
В силу данной теоремы вводится следующее (основное)
Определение 4.1. Матрица 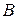 называется обратной по отношению к матрице
называется обратной по отношению к матрице  , если
, если
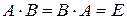 . (4.1)
. (4.1)
В силу равенств (4.1) матрица  является обратной к матрице
является обратной к матрице 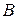 , то есть
, то есть  и
и 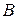 являются взаимно обратными матрицами.
являются взаимно обратными матрицами.
Обратная к  матрица обозначается символом
матрица обозначается символом 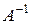 . Таким образом,
. Таким образом, 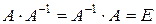 .
.
Если определитель матрицы равен нулю, то такую матрицу принято называть вырожденной, в противном случае – невырожденной.
Пусть матрица  является невырожденной, то есть
является невырожденной, то есть 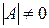 . Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы
. Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы  :
:
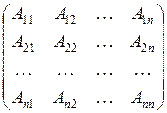 .
.
При транспонировании её получается матрица 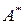 , называемая присоединенной к матрице
, называемая присоединенной к матрице  :
:
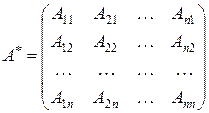 .
.
Теорема 4.2. Для того чтобы для матрицы  существовала обратная матрица
существовала обратная матрица 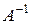 , необходимо и достаточно, чтобы матрица
, необходимо и достаточно, чтобы матрица  была невырожденной и при этом
была невырожденной и при этом
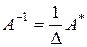 , (4.2)
, (4.2)
где 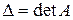 .
.
Доказательство необходимости. Если существует обратная матрица 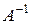 , то
, то 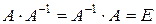 . Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем:
. Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем: 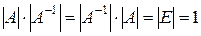 . Но это означает, что
. Но это означает, что 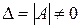 .
.
Доказательство достаточности. Перемножая матрицы  и
и 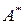 , в силу теорем 3.1 и 3.2 получаем
, в силу теорем 3.1 и 3.2 получаем
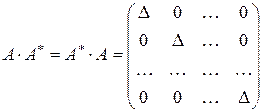 или
или 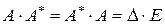 .
.
Отсюда следует, что матрица 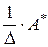 является обратной по отношению к матрице
является обратной по отношению к матрице  , то есть имеет место формула (4.2). ■
, то есть имеет место формула (4.2). ■
Пример 1. Дана матрица
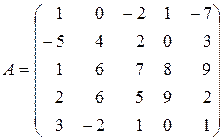 .
.
Выяснить, существует ли обратная матрица 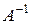 .
.
Решение. Вычислим определитель матрицы  . Прибавив к первой строке определителя матрицы
. Прибавив к первой строке определителя матрицы  его третью строку, получим определитель
его третью строку, получим определитель
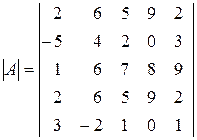 ,
,
у которого первая и четвертая строки совпадают. А это значит, что определитель равен нулю.
Итак, матрица  вырожденная, и, следовательно, обратная матрица
вырожденная, и, следовательно, обратная матрица 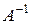 не существует.
не существует.
Пример 2. Для матрицы
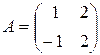
найти обратную матрицу.
Решение. Вычислив определитель данной матрицы
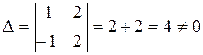 ,
,
можем утверждать, что обратная матрица для неё существует.
Найдём для каждого элемента 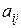 матрицы
матрицы  его алгебраическое дополнение
его алгебраическое дополнение 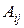 :
:
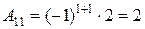 ; ; | 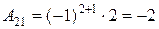 ; ; |
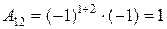 ; ; | 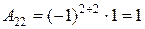 . . |
По формуле (4.2) найдём обратную матрицу
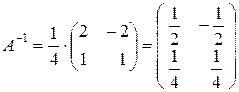 .
.
Проверка:
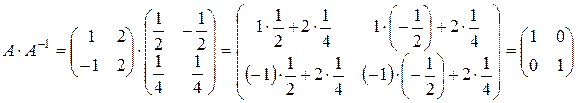 .
.
Пример 3. Найти матрицу, обратную к матрице
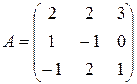 .
.
Решение. Вычислим определитель матрицы 
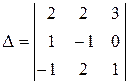 .
.
Прибавив к элементам второго столбца соответствующие элементы первого столбца, получим
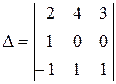 .
.
Разложим определитель по элементам второй строки:
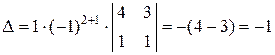 .
.
Итак, 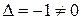 . То есть матрица
. То есть матрица  является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица
является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица 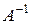 .
.
Найдем для каждого элемента матрицы  его алгебраическое дополнение:
его алгебраическое дополнение:
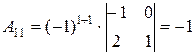 , , | 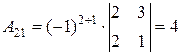 , , | 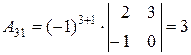 , , |
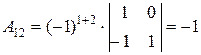 , , | 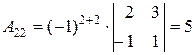 , , | 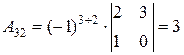 , , |
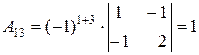 , , | 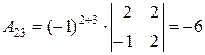 , , | 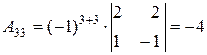 . . |
Составим присоединённую матрицу
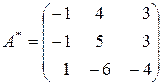 ,
,
и по формуле (4.2) найдём обратную матрицу
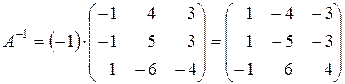 .
.
Проверка:
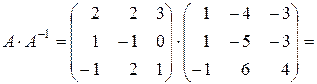
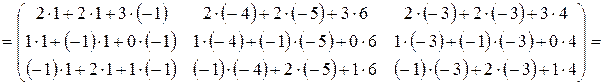
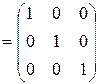 .
.
Пример 4. Дана матрица
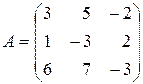 .
.
Определить, существует ли обратная матрица 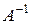 , и если существует, то найти её.
, и если существует, то найти её.
Решение. Определитель матрицы 
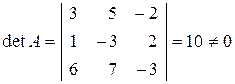 .
.
Следовательно, данная матрица невырожденная, и 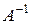 существует. Согласно формуле (4.2),
существует. Согласно формуле (4.2),
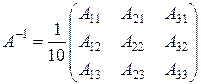 .
.
Найдём алгебраические дополнения элементов данной матрицы:
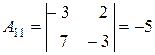 , , | 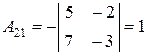 , , | 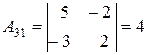 , , |
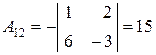 , , | 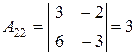 , , | 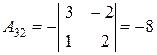 , , |
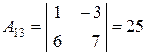 , , | 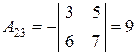 , , | 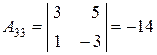 . . |
Тогда
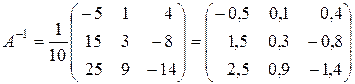 .
.
Проверка:
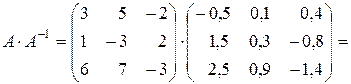
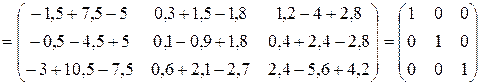 .
.
Пример 5. Для матрицы
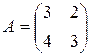
найти обратную матрицу.
Решение. Рассмотрим матричное уравнение
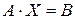 , (4.3)
, (4.3)
где
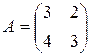 ,
, 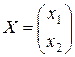 ,
, 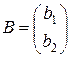 .
.
Умножив обе части уравнения (4.3) на матрицу 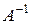 слева, получим
слева, получим
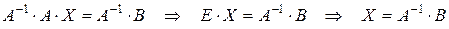 . (4.4)
. (4.4)
Выражение (4.4) есть решение уравнения (4.3), которое в скалярной форме имеет вид:
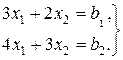 (4.5)
(4.5)
Решая систему (4.5), получаем
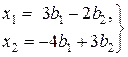
или, что то же самое,
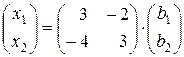 . (4.6)
. (4.6)
Выражение (4.6) есть (4.4). Следовательно,
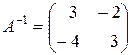 .
.
Проверка:
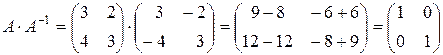 .
.
Пример 6. Решить матричное уравнение
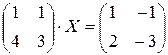 . (4.7)
. (4.7)
Решение. Пусть
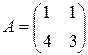 ,
, 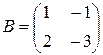 .
.
Тогда исходное уравнение запишется в виде
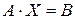 . (4.8)
. (4.8)
Умножая обе части уравнения (4.8) слева на матрицу 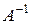 , получаем
, получаем
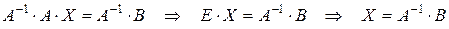 . (4.9)
. (4.9)
Вычислим обратную матрицу 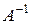 , для чего найдем определитель
, для чего найдем определитель 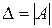 и алгебраические дополнения элементов матрицы
и алгебраические дополнения элементов матрицы  :
:
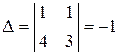 ,
, 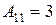 ,
, 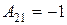 ,
, 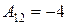 ,
, 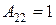 .
.
Итак,
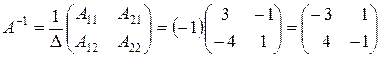 .
.
Проверим верность полученного результата:
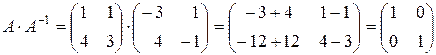 .
.
Таким образом, обратная матрица 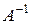 вычислена верно.
вычислена верно.
Подставляя 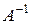 в выражение (4.9), получаем
в выражение (4.9), получаем
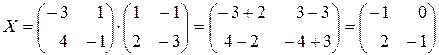 .
.
Проверка:
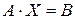
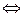
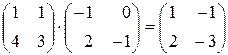
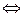
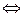
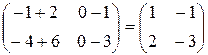
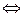
 .
.
Получили тождественное равенство. Следовательно, уравнение (4.7) решено верно: 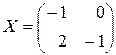 .
.
ЗАДАЧИ
1.10. Найти обратные матрицы для следующих матриц:
1) 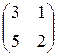 ; ; | 4) 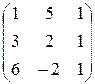 ; ; | 7) 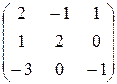 ; ; |
2) 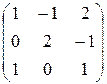 ; ; | 5) 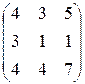 ; ; | 8) 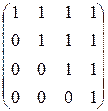 ; ; |
3) 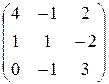 ; ; | 6) 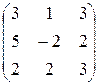 ; ; | 9) 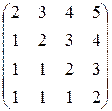 . . |
1.11. Вычислить:
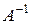 ,
, 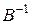 ,
, 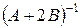 ,
, 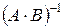 ,
, 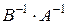 ,
, 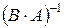 ,
, 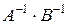 ,
, 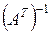 ,
, 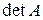 ,
, 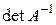 ,
, 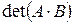 , если:
, если:
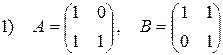 ;
; 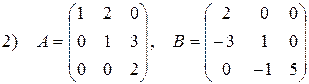 .
.
 2015-03-22
2015-03-22 2417
2417