Поступательное движение

Кинематика поступательного движения

При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.

Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.

Линию, по которой движется материальная точка в пространстве, называют траекторией.

Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ?r=r-r₀, направленный от положения точки в начальный момент времени к ее положению в конечный момент.

Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.

Поступательное движение

В кинематике, как и в статистике, будем рассматривать все твердые тела как абсолютно твердые.

Абсолютно твердым телом называется материальное тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между любыми двумя его точками остается постоянным.

Кинематика твердого тела, также как и динамика твердого тела, является одним из наиболее трудных разделов курса теоретической механики.

Задачи кинематики твердого тела распадаются на две части:

1) задание движения и определение кинематических характеристик движения тела в целом;

2) определение кинематических характеристик движения отдельных точек тела.

Существует пять видов движения твердого тела:

1) поступательное движение;

2) вращение вокруг неподвижной оси;

3) плоское движение;

4) вращение вокруг неподвижной точки;

5) свободное движение.

Первые два называются простейшими движениями твердого тела.

Начнем с рассмотрения поступательного движения твердого тела.

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.

Поступательное движение не следует смешивать с прямолиней­ным. При поступательном движении тела траектории его точек мо­гут быть любыми кривыми линиями.

Приведем примеры:

1. Кузов автомобиля на прямом горизонтальном участке дороги движется поступательно. При этом траектории его точек будут пря­мыми линиями.

2. Спарник АВ (рис.3) при вращении кривошипов O₁A и O₂B также движется поступательно (любая проведенная в нем прямая остается параллельной ее начальному направлению). Точки спарника движутся при этом по окружностям.

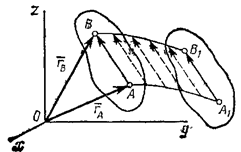
Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению ско­рости и ускорения.

Размерность 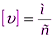. Средняя скорость вдоль траектории – это скалярная величина.

Есть понятие средней скорости перемещения: это отношение модуля перемещения к времени движения тела:
.
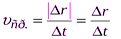Для определения скорости тела (материальной точки) в данный момент времени в данной точке траектории вводится понятие мгновенной скорости. Предел отношения 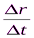при неограниченном уменьшении промежутка времени называется мгновенной скоростью:
,
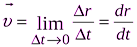где 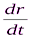– производная от вектора перемещения по времени.
Мгновенная скорость – величина векторная, направленная по касательной к траектории движения.

Модуль мгновенной скорости определяется выражением:

,
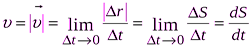где 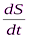– производная пути по времени.

Среднее ускорение:

 

.

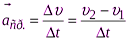Ускорение численно равно изменению скорости в единицу времени. Размерность:

.

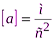Мгновенное ускорение:

 

.

 

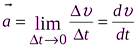При прямолинейном движении величина мгновенного ускорения

;

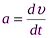величина среднего ускорения

.

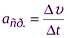2.

Нормальное и тангенциальное ускорения

Ускорение – это векторная величина, которая характеризует быстроту изменения скорости.

Составляющая а_τ вектора ускорения, направленная вдоль касательной к траектории в данной точке, называется тангенциальным (касательным) ускорением. Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор а_τ направлен в сторону движения точки при возрастании ее скорости и в противоположную сторону - при убывании скорости.

Тангенциальная составляющая ускорения а_τ равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю:

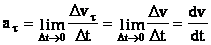
Вторая составляющая ускорения, равная:

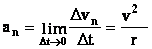
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют так же центростремительным ускорением).

Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих:

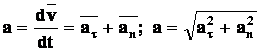
Тангенциальная составляющая ускорения:

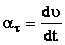; υ = ω·R, поэтому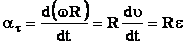

Нормальная составляющая ускорения:

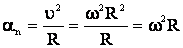
Таким образом, связь между линейными и угловыми величинами выражается следующими формулами: S = R·φ, υ = ω·R, a_τ = R·ε, a_n = ω²·R.

3.

Определение пути при различных видах движения

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Угловая скорость вращения тела — векторная величина.

.

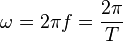Частота вращения (угловая частота) — число оборотов в единицу времени.

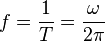
5.

Поступательное движение	Вращательное движение
Перемещение	S	Угловое перемещение	φ
Линейная скорость		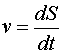Угловая скорость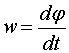
Ускорение		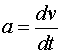Угловое ускорение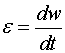
Масса	m	Момент инерции	I
Импульс		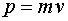Момент импульса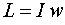
Сила	F	Момент силы	M

9.

Законы природы, определяющие изменение состояния движения механических систем, не зависят от того, к какой из двух инерциальных систем отсчета они относятся. Это и есть принцип относительности Галилея.

Из преобразований Галилея и принципа относительности следует, что взаимодействия в классической физике должны передаваться с бесконечно большой скоростью c = ∞, т. к. в противном случае можно было бы одну инерциальную систему отсчета отличить от другой по характеру протекания в них физических процессов.

Принцип относительности Галилея и законы Ньютона подтверждались ежечасно при рассмотрении любого движения, и господствовали в физике более 200 лет.
Но вот в 1865 г. появилась теория Дж. Максвелла, и уравнения Максвелла не подчинялись преобразованиям Галилея.

Ее мало кто принял сразу, она не получила признания при жизни Максвелла. Но вскоре все сильно изменилось, когда в 1887 г., после открытия электромагнитных волн Герцем, были подтверждены все следствия, вытекающие из теории Максвелла, – ее признали. Появилось множество работ, развивающих теорию Максвелла.