2015-03-22
600
Пусть при некоторых углах атаки aи скольжения b, а также заданных параметрах набегающего потока (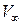
, 
, 
, 
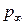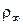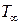) известны распределения давления 
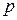и касательных напряжений 
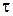по поверхности обтекаемого тела. Требуется определить суммарные величины составляющих аэродинамической силы и момента.
|
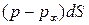и касательная к площадке сила 
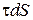(рис. 10.1). Сумма проекций этих сил на ось ОX поточной системы координат равна
,
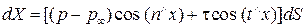где n – нормаль; t – касательная к площадке dS. Проекции от действия этих напряжений на оси ОY и ОZ можно записать аналогично. Чтобы получить суммарные силы, необходимо проинтегрировать по всей поверхности S. Введем коэффициент давления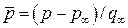 
, местный коэффициент трения 
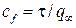и характерную площадь 
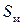(площадь крыла, миделя и др.).
После подстановок получим в обозначениях для скоростной системы координат следующие интегральные выражения для проекций аэродинамической силы:
,
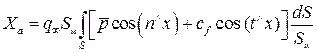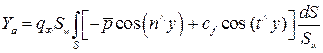, (10.4)
.
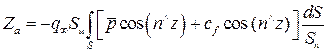Интегралы в формулах (10.4) представляют собой безразмерные величины, учитывающие влияние на аэродинамические силы характера обтекания тела заданной геометрической формы и распределения безразмерных коэффициентов давления и трения по его поверхности. Их обозначают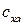 
, 
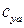и 
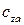– коэффициенты силы лобового сопротивления, подъемной силы и боковой силы. То есть
.
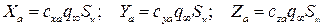Подобным образом получаются и общие соотношения для моментов:
,
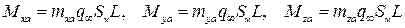где L – характерный геометрический размер (плечо силы);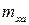 
– коэффициент момента крена; 
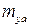– коэффициент момента рыскания; 
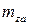– коэффициент момента тангажа. Аналогично можно вывести соотношения для коэффициентов сил и моментов в связанной системе координат.
Анализ выражений для аэродинамических сил (10.4) показывает, что каждую из этих сил можно представить в виде суммы двух составляющих:
– первая из них обусловлена аэродинамическим давлением (присуща как идеальной, так и реальной жидкости);
– вторая обусловлена касательными напряжениями (присуща только для реальной, вязкой жидкости).
Тогда, например, подъемную силу можно представить в виде суммы:
,
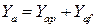где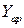 
– подъемная сила, обусловленная аэродинамическим давлением; 
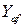– подъемная сила, обусловленная трением.
Или в коэффициентах:
.
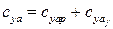Аналогично из двух составляющих можно представить лобовое сопротивлени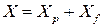е: 
, где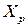 
– сопротивление давления; 
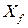– сопротивление трения. Или для коэффициента лобового сопротивления: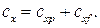 
В случае симметричного обтекания (a = 0) силы, обусловленные трением и давлением, с противоположных сторон тела взаимно компенсируются, и подъемная сила равна нулю. Поэтому подъемная сила появляется только в случае, когда a ¹0.
Составляющие аэродинамических сил и моментов, зависящие от трения, не всегда по порядку величин такие же, как составляющие от давления. Влияние трения оказывается существенным при обтекании длинных и тонких тел, и в практических случаях влияние трения наиболее существенно для определения силы лобового сопротивления или продольной силы.
