1. Методы Эйлера численного решения дифференциальных уравнений первого и второго порядков.
Метод численного решения дифференциального уравнения первого порядка
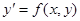 (1)
(1)
с начальным условием 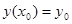 основан на разложении решения в ряд Тейлора в
основан на разложении решения в ряд Тейлора в 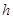 -окрестности точки
-окрестности точки 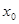 :
:
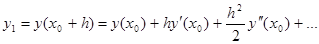
При отбрасывании всех членов ряда, содержащих производные второго и высших порядков получим: 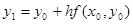 , где
, где 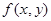 -правая часть уравнения (1).
-правая часть уравнения (1).
Пользуясь значением 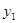 из разложения
из разложения 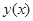 в
в 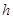 - окрестности точки
- окрестности точки 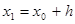 получим
получим
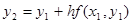 (2)
(2)
Аналогично продолжая для следующей точки 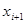 , получим
, получим
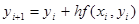 (3)
(3)
Если дано уравнение второго порядка
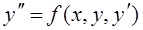 (4)
(4)
с начальными условиями 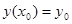 и
и 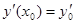 , то как такое уравне- ние можно свести к системе двух уравнений первого порядка
, то как такое уравне- ние можно свести к системе двух уравнений первого порядка
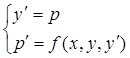 , (5)
, (5)
причем 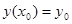 и
и 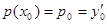 .
.
Тогда приближенные значения функций 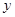 и
и 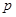 в точке
в точке 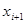 можно высислить по формулам
можно высислить по формулам
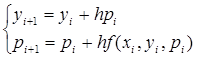 , (6)
, (6)
где 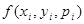 - правая часть уравнения (4).
- правая часть уравнения (4).
При достаточно малой величине шага 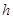 метод Эйлера дает решение с большой точностью, т.к. погрешность решения близка к
метод Эйлера дает решение с большой точностью, т.к. погрешность решения близка к 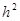 .
.
2. Методы Рунге-Кутта численного решения дифференциальных уравнений первого и второго порядков.
Пусть дано дифференциальное уравнение первого порядка 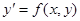 с начальным условием
с начальным условием 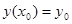 .
.
Последовательные значения 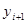 искомой функции
искомой функции 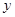 определяются по формуле
определяются по формуле 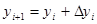
где 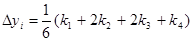 ,
,
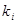 - коэффициенты, которые вычисляются по формулам
- коэффициенты, которые вычисляются по формулам
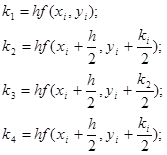
где 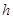 - шаг интегрирования;
- шаг интегрирования;
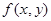 - правая часть дифференциального уравнения, разрешенного относительно производной.
- правая часть дифференциального уравнения, разрешенного относительно производной.
Если дано уравнение второго порядка 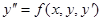 с начальными условиями
с начальными условиями 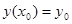 и
и 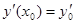 , то как такое уравне- ние можно свести к системе двух уравнений первого порядка
, то как такое уравне- ние можно свести к системе двух уравнений первого порядка
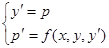 ,
,
причем 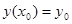 и
и 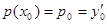 .
.
Тогда приближенные значения функций 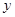 и
и 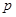 можно вычис- лить по формулам
можно вычис- лить по формулам
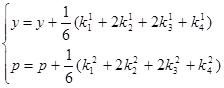 ,
,
где 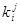 - коэффициенты вычисляемые по формулам
- коэффициенты вычисляемые по формулам
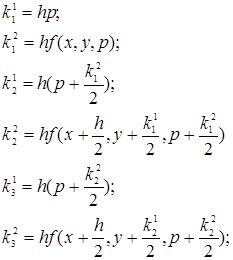
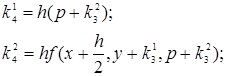 ,
,
где 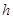 - шаг интегрирования;
- шаг интегрирования;
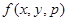 - правая часть дифференциального уравнения, разрешенного относительно производной.
- правая часть дифференциального уравнения, разрешенного относительно производной.
Метод Рунге-Кутта применим также для приближенного решения систем обыкновенных дифференциальных уравнений, применяя формулы для каждого уравнения в отдельности. При этом погрешность интегрирования - есть величина порядка 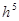 .
.
 2015-03-22
2015-03-22 379
379








