Учет инфляционного обесценения денег в принятии финансовых решений

Пусть S_a — сумма, покупательная способность которой с уче­том инфляции равна покупательной способности суммы при от­сутствии инфляции. Через Δ S обозначим разницу между этими суммами.

Отношение Δ S /S, выраженное в процентах, называется уров­нем инфляции.

При расчетах используют относительную величину уровня ин­фляции — темп инфляции .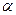

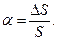
Тогда для определения S_a получаем следующее выражение:

S_α = S+ ΔS= S+ S 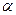= S( 1 + 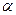). (3.5)

Величину (1 + 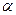), показывающую, во сколько раз S_a больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции I _и.

I _и = 1 + .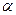

Динамика индекса инфляции за несколько лет отражает изме­нения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по срав­нению с предыдущим таким же периодом указывает на ускорение инфляции, снижение — на уменьшение ее темпов.

Пусть 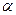– годовой уровень инфляции. Это значит, что через год сумма 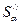будет больше суммы 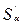в (1 + 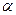) раз. По прошествии еще одного года сумма 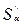будет больше суммы S'_a в (1 + 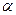) раз, т. е. больше суммы S в (1+ 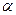)² раз. Через п лет сумма 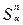вырастет по отношению к сумме S в(1 + 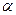) ⁿ раз. Отсюда видно, что инфля­ционный рост суммы S при годовом уровне инфляции 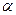– то же самое, что наращение суммы S по сложной годовой ставке про­центов .

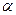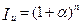. (3.6)

Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.).

Очень важно запомнить данную аналогию со сложным процентом, так как одна из наиболее часто встречающихся ошибок, связанных с расчетом уров­ня инфляции за некоторый период, связана именно с не­учетом данного обстоятельства.